線対称との違いは!?｢点対称｣な図形を理解しよう！

図形問題は得意ですか？ なかには「点対称」や「線対称」と言われても、なにがどう違うのか全くもってお手上げの人もいるでしょう。ただ、点対称は覚えるべき基本が少なく、得点につながりやすい単元といえます。線対称との違いや、基本をおさえていきましょう。

点対称な図形は1点を中心に180度回転させても同じ形

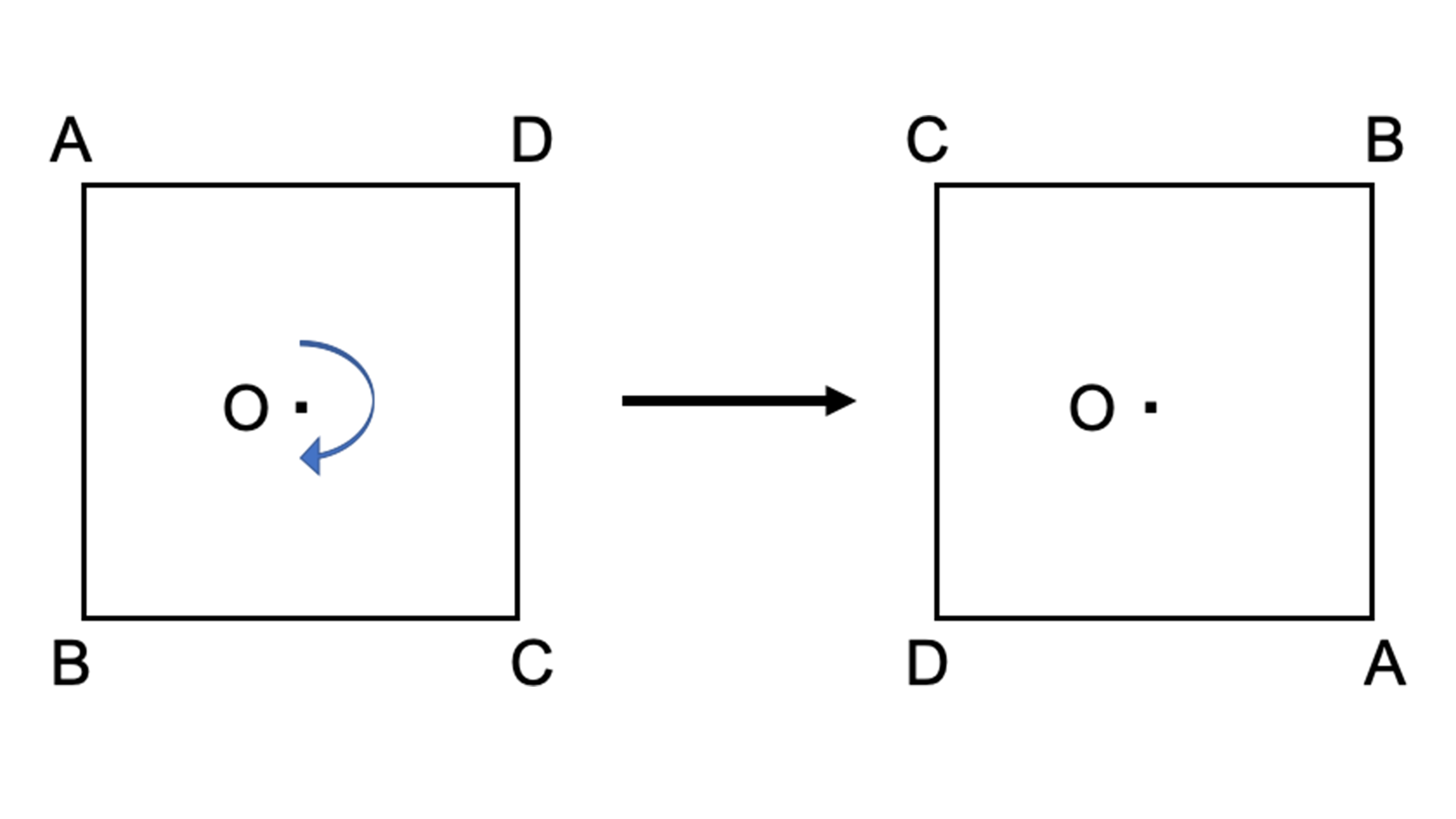
点対称とは、ある1点を中心として図形を180度回転させたとき、元の図形と回転させた図形がピッタリ重なる関係を示します。たとえば上図の左側にある
図形：正方形ABCDを点Oを中心として180度回転させてみましょう。すると回転させた前後で全く形が変わらない(右図)のが分かるのではないでしょうか。
点対称のとき、点や辺に対して特別な呼び方が使われます。要は、回転させたときに重なり合うものを呼ぶときに「対称の○○」と呼ぶという決まりです。問題文などで出てきますので、上の図を見ながら確認してみましょう。

-----------------------------------
■対称の中心：図形を180度回転させたときに中心にくる点(上の図では点O)
■対応する点：図形を180度回転させたときに重なり合う点(上の図では左図A→右図C / 左図B→右図D / 左図C→右図A / 左図D→右図B)
■対応する辺：図形を180度回転させたときに重なり合う辺(上の図では左図AB→右図CD / 左図BC→右図DA / 左図CD→右図AB /左図DA→右図BC)
■対応する角：図形を180度回転させたときに重なり合う角
(上の図では左図∠ABC→右図∠CDA / 左図∠BCD→右図∠DAB /左図∠CDA→右図∠ABC / 左図∠DAB→右図∠BCD)
-----------------------------------
また点対称の図形には下のような性質があります。
-----------------------------------
(点対称の性質1)対応する点同士を直線で結び合わせると対称の中心を通る
(点対称の性質2)対応する点と対称の中心を結ぶ直線2本は長さが同じ
-----------------------------------

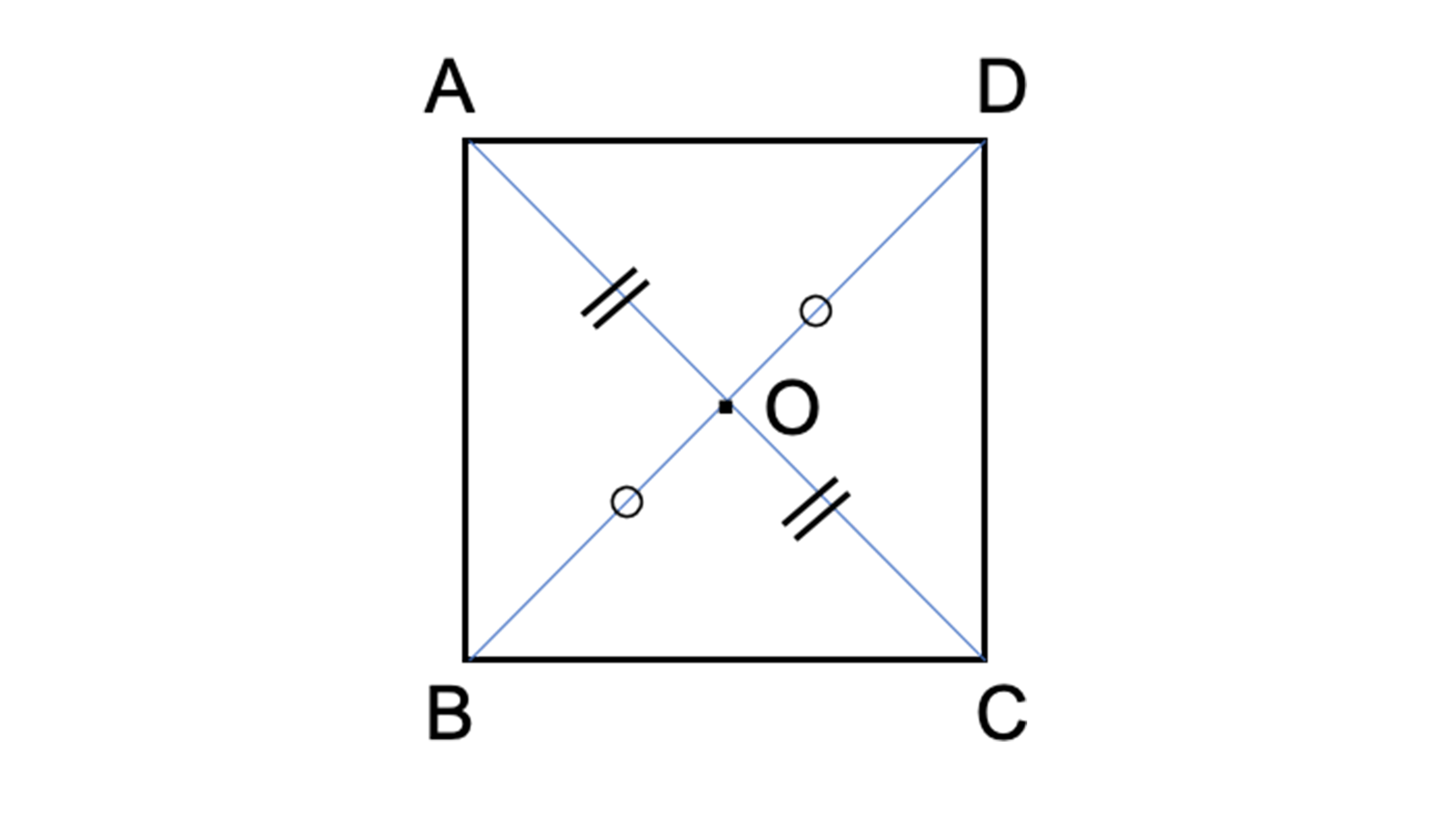
性質(1)(2)とはどういう意味なのでしょうか。先ほどの説明でも使った正方形ABCDを使って説明してみましょう。正方形ABCDは原点Oを中心とした点対称の図形のため、対角線を引くと対応する点同士(AとC、BとD)が結べました。点対称の性質をアルファベットなどで示すと下のようになります。このように対応する点同士を結び合わせて関係性を考えてみましょう。

-----------------------------------
・ACとBDが原点Oで交わっている→(1)
・AO=CO(BO=DO)→(2)
-----------------------------------
また点対称な図形の見分け方を改めてまとめてみました。
-----------------------------------
①180度回転させる→同じ形になる
②対応する(と思われる)点同士をすべて直線で結ぶ→直線が1点(対称の中心)ですべて交わる
③対応する(と思われる)点1組を直線でつなげる(このとき対称の中心と思われる点を通らなければ点対称ではない)→対応する(と思われる)点と対称の中心の間の距離が等しい(片方の点と対称の中心を結んだ直線ともう片方と対称の中心を結んだ直線の長さが同じ)
-----------------------------------

①は切り抜いた図形を使って確認できたり、マス目を利用して確認できたりする際には便利でしょう。また②は結んだ直線が2本だけのときは点対称にならない場合があります。3本以上の線を引くか、③を合わせて活用しましょう。

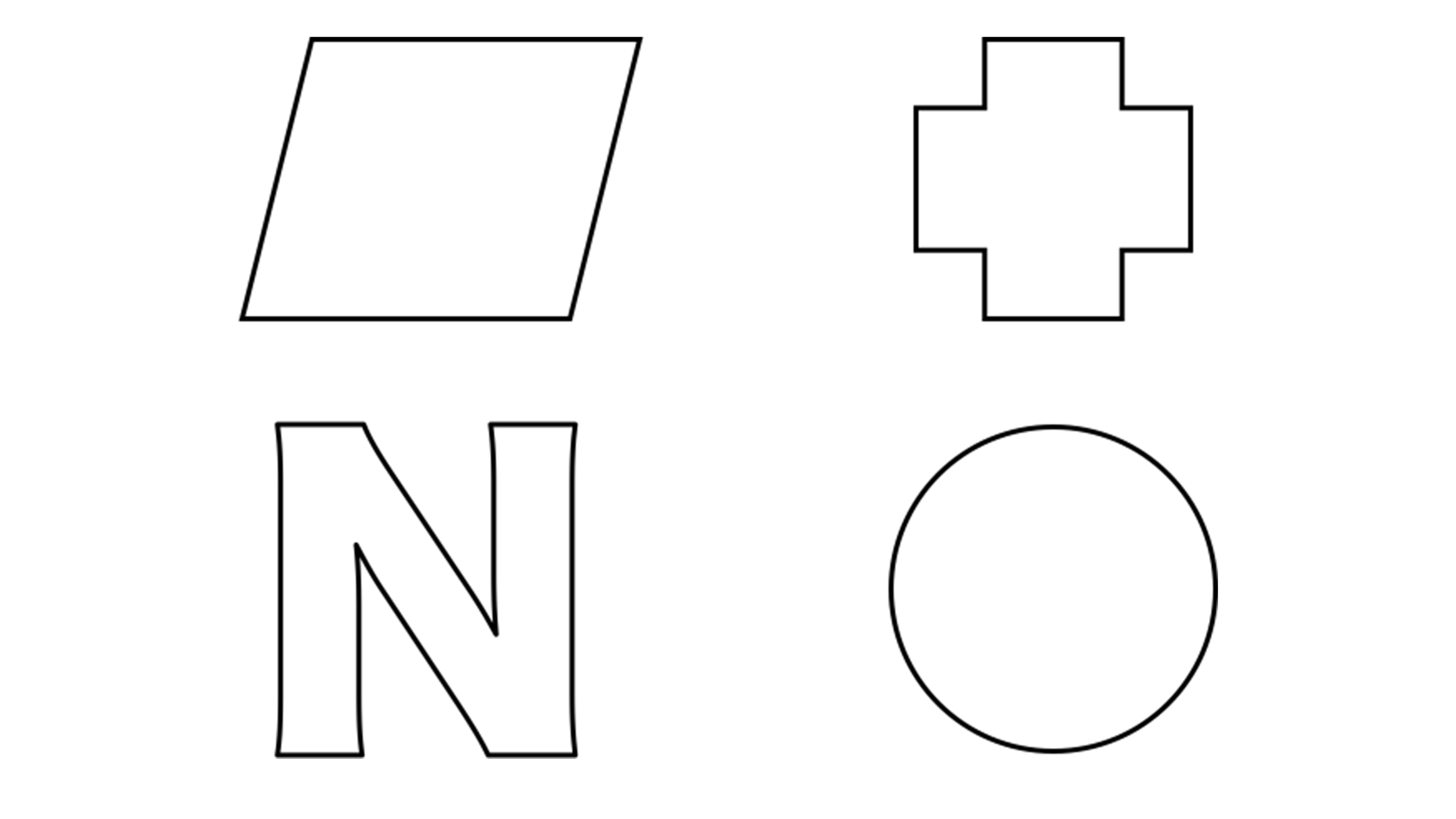
また正方形を例にして説明してきましたが、正六角形や正十角形など頂点の数が偶数の正多角形の場合は点対称になります。逆を言えば頂点の数が奇数の正多角形は点対称ではありません。覚えておけば、線を書き入れたりせずとも点対称かどうか見分けられるので便利でしょう。ほかにも点対称の図形は無限に作れます。下のような図形も点対称ですので、線を書き入れて確かめてみてください。

点対称な図形と線対称な図形の違いは？

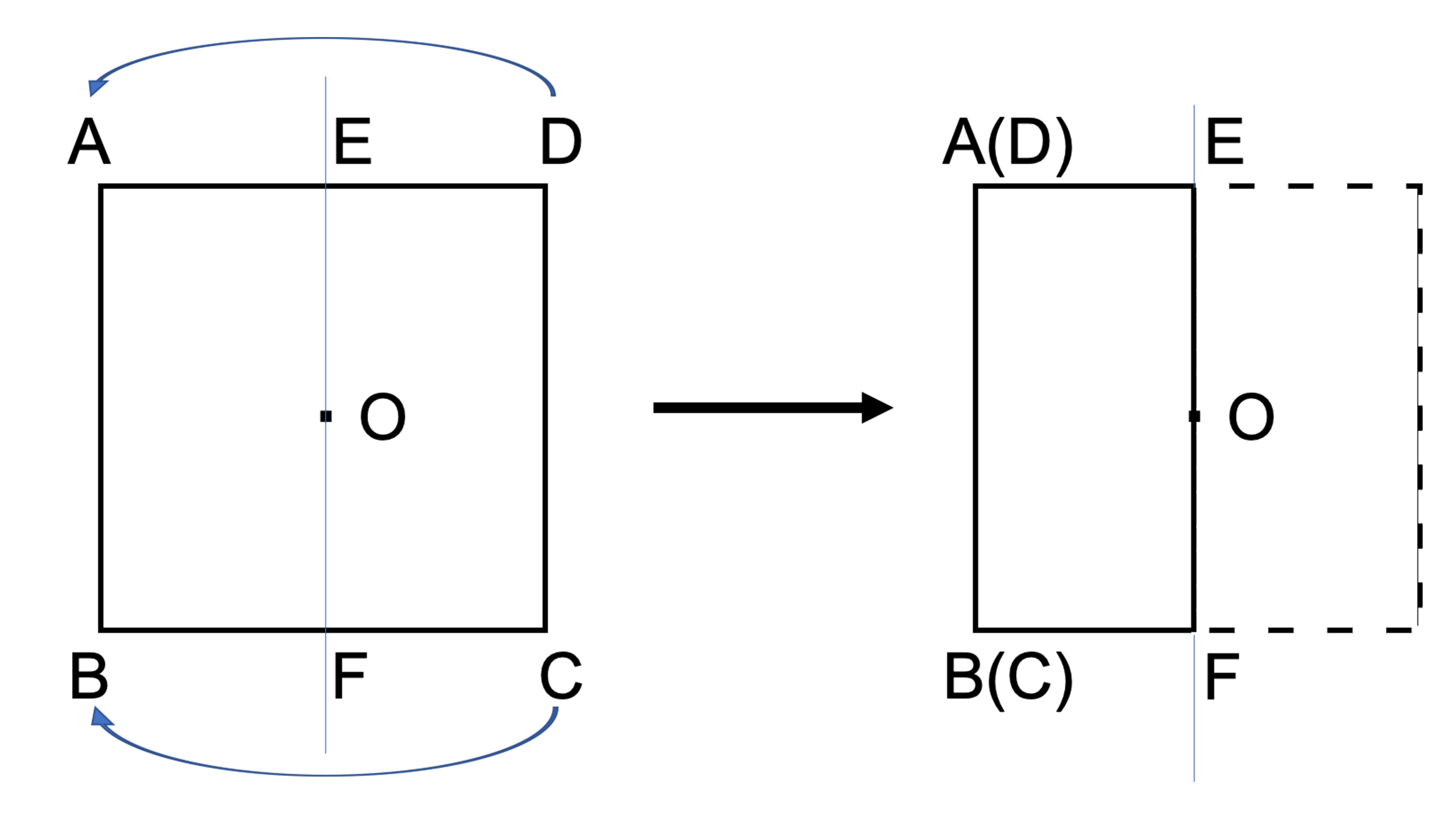
そして点対称と似ていて間違えやすい「線対称」についても簡単に説明しましょう。線対称とは、1本の直線を軸として2つ折りにした際に両側がピッタリと重なり合う図形を指します。正方形ABCDもたとえば直線EFを軸として折り合わせるとピッタリ重なります(正方形のような頂点の数が偶数の正多角形は点対称かつ線対称です)。

また直線EFのように線対称の軸となる直線を「対称軸」と呼ぶのを覚えてください。さらに点対称と同じく、線対称でも“対応する辺”や“対応する点”という言葉を使います。加えて線対称になる図形の性質も挙げられますので合わせて覚えておきましょう。

-----------------------------------
(線対称の性質1)対応する点2つを結ぶ直線は、対称軸と垂直に交わる
(線対称の性質2)その交点から、対応する2つの点までの距離は等しい
-----------------------------------

では、点対称と線対称はどのような違いがあるのでしょうか。それぞれの性質を言葉でまとめましたが、図形と記号にまとめた方がわかりやすいかもしれません。下図をご覧ください。左が線対称、右が点対称です。

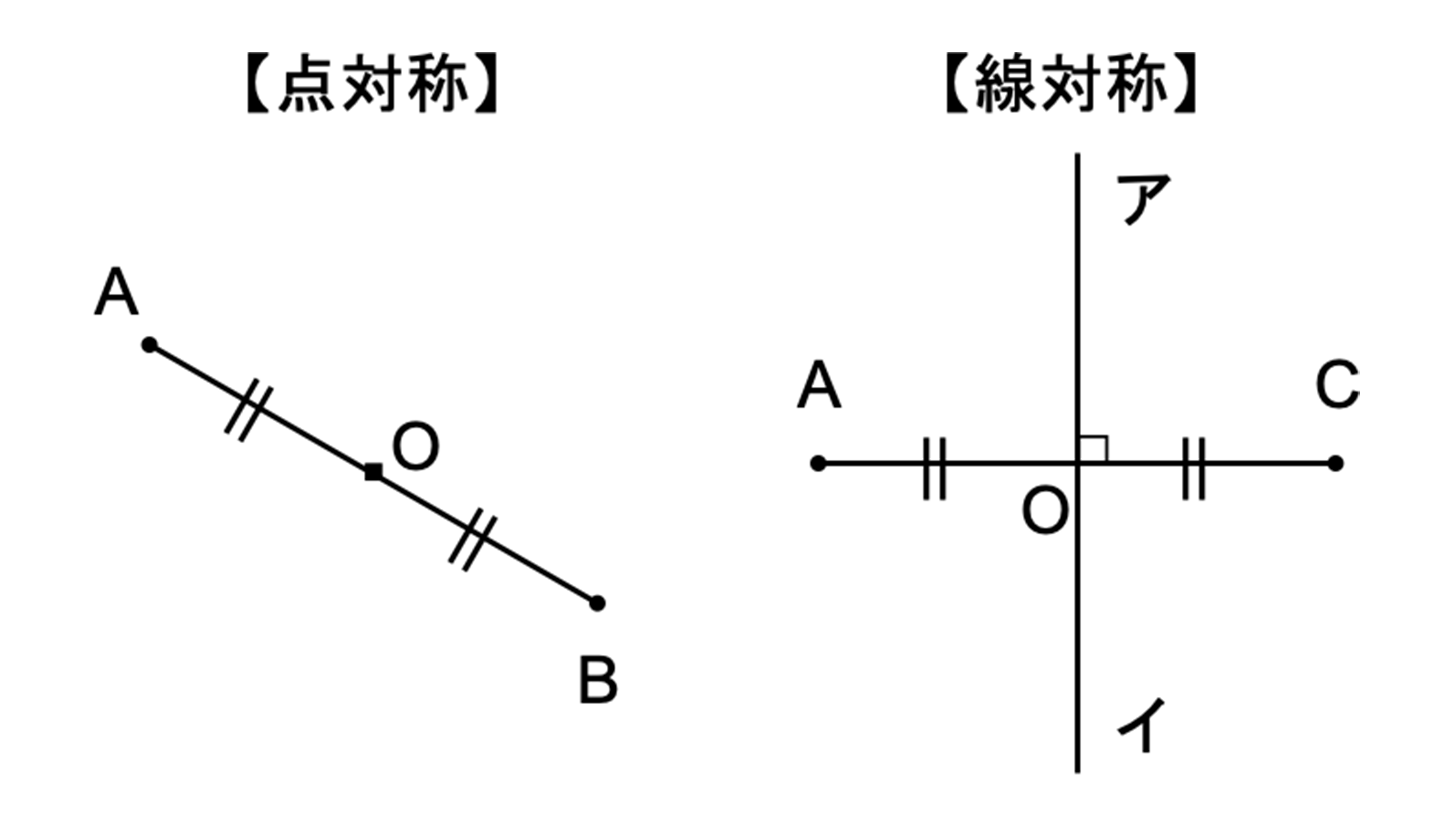
上の図にならって性質を書き変えると下のようになります。先ほどのような文章で覚えるよりもこちらの方が短くて覚えやすいのではないでしょうか。

【点対称】
AB上に点Oがある ←(点対称の性質1)
AO＝BO ←(点対称の性質2)

【線対称の性質】
AC⊥アイ　←(線対称の性質1)
AO=CO　←(線対称の性質2)
そして線対称と点対称の図形を見分ける問題はテストなどでよく聞かれます。下の手順で見分けてみましょう。
-----------------------------------
①図形に縦線を入れる
↓
②図形を180度回転させる(①でできた、直線と図形の交点を上から下まで回して移動するイメージ)
→180度回転させたときに元の図形と同じ形になれば「点対称」
→180度回転させる間に左右が同じ形になるときがあれば「線対称」(左右対称になる回数＝対称軸になる直線の本数)
-----------------------------------

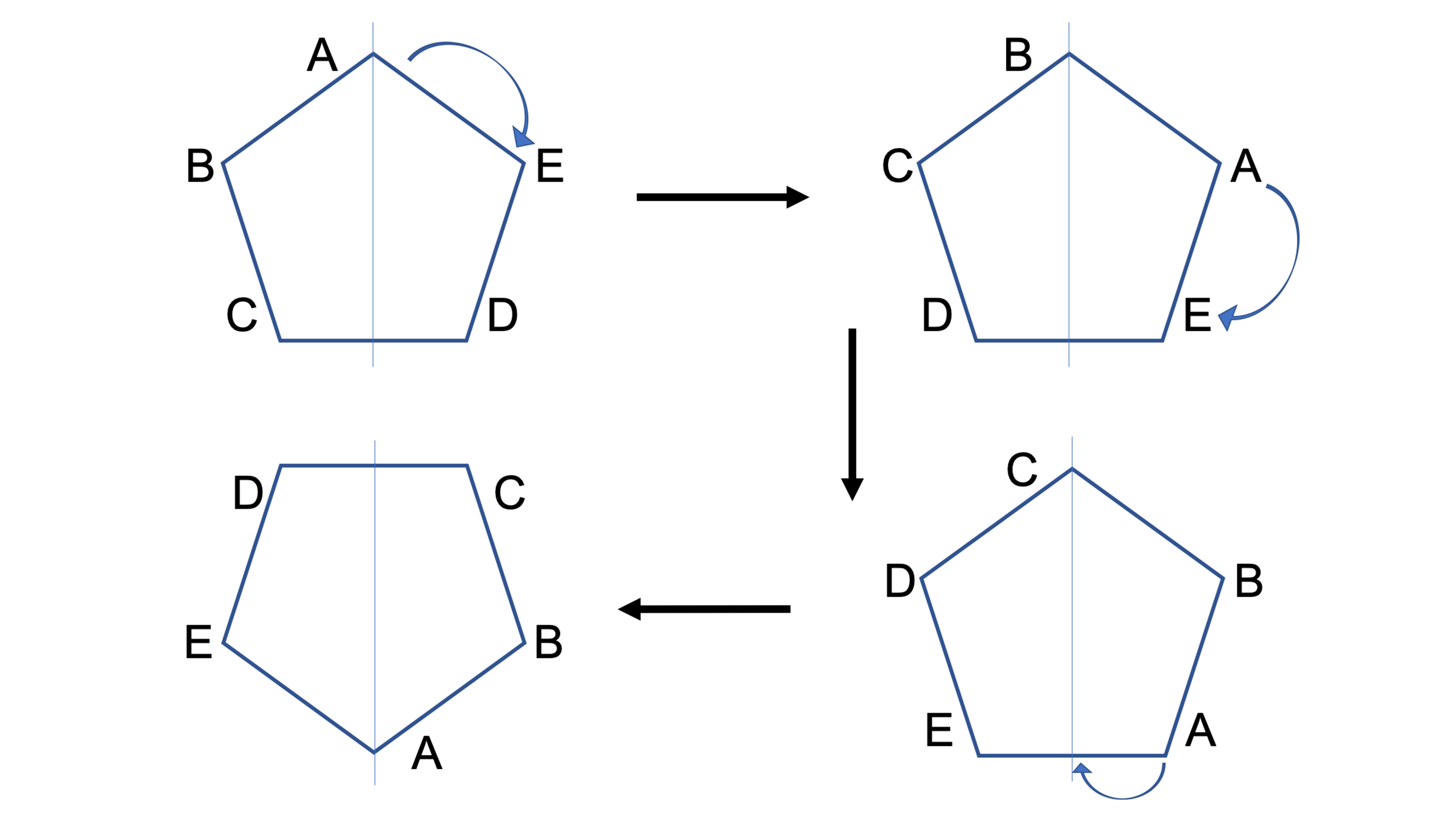
台形ABCDEを例にして実際にやってみましょう。まず台形ABCDEの頂点Aが交点となるように縦線を引きます(左上)。そこからAを時計回りに180度回転させます(右上→右下)。180度回転してAが縦線と交わりました(左下)。左上がスタートであり、右上・右下・左下のタイミングで左右対称になっています。そのため台形ABCDEは線対称といえます。ただ、左上と左下を比べても違う形になっているため、台形ABCDEは点対称とは言えません。このように点対称と線対称を見分けましょう。

ほかにも問題の条件によっては、点対称・線対称の性質に当てはめて考えた方がわかりやすい場合もあります。問題演習をこなしていく間に多くのパターンに触れて、慣れていきましょう。

点対称な図形の作図方法

点対称については図形を作図する問題も出題されます。たとえば下のような問題です。

Q：点Oを対称の中心として、点対称な図形を書きなさい。

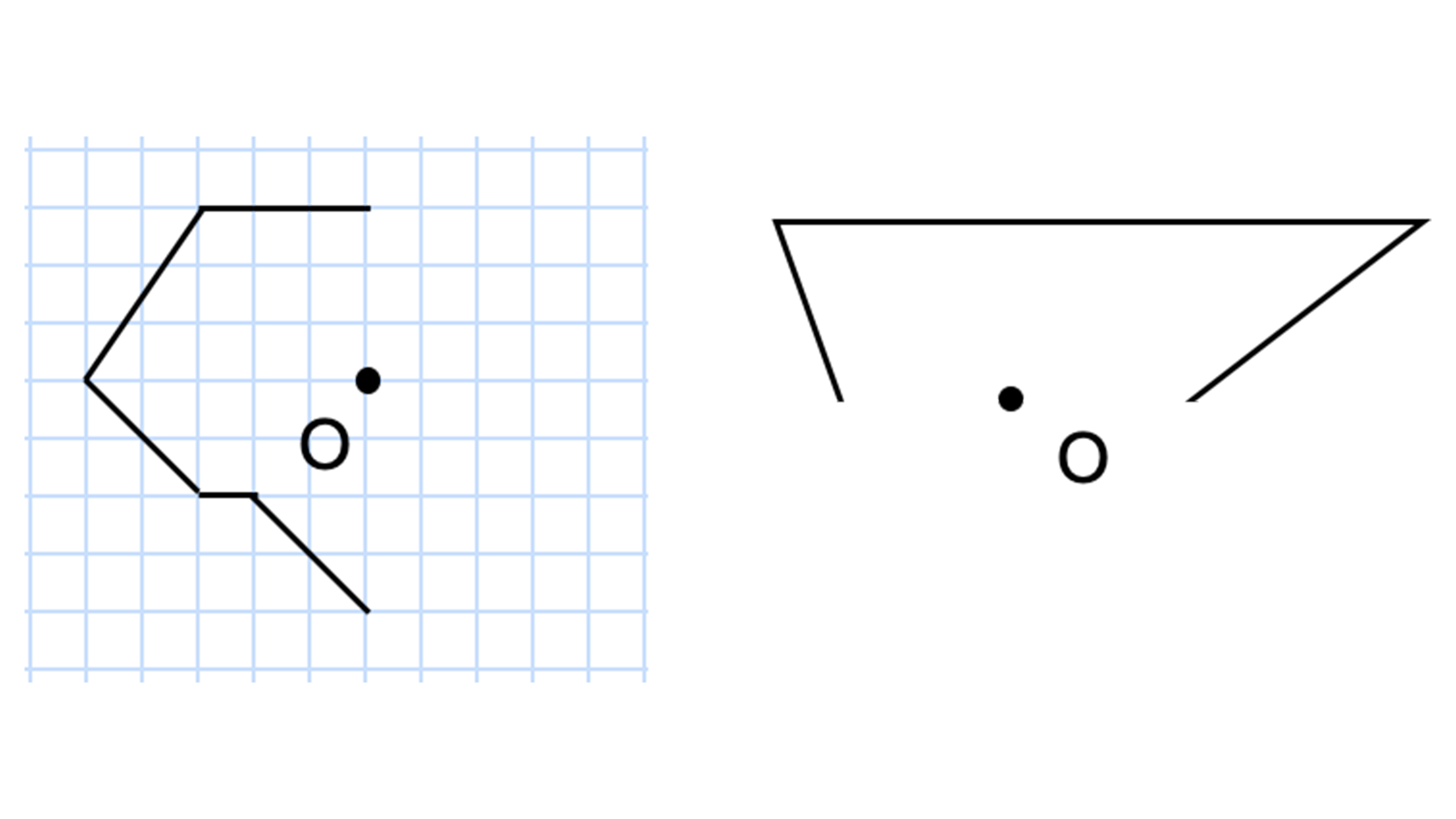
【作図方法①：マス目がある場合】
左側のようにマス目がある問題は、「点対称の性質2：対応する点と対称の中心を結ぶ直線2本は長さが同じ」を利用すると作図しやすいです。下のように、ある点から原点まで進む場合の縦横のマス目を数えます(下の場合は縦横ともに3マス)。そして、それと同じ数だけ原点から進んだ点が対応する点の位置です。元の図形のすべての点で同じ作業をすれば点対称の図形が完成します(完成図は下の右図)

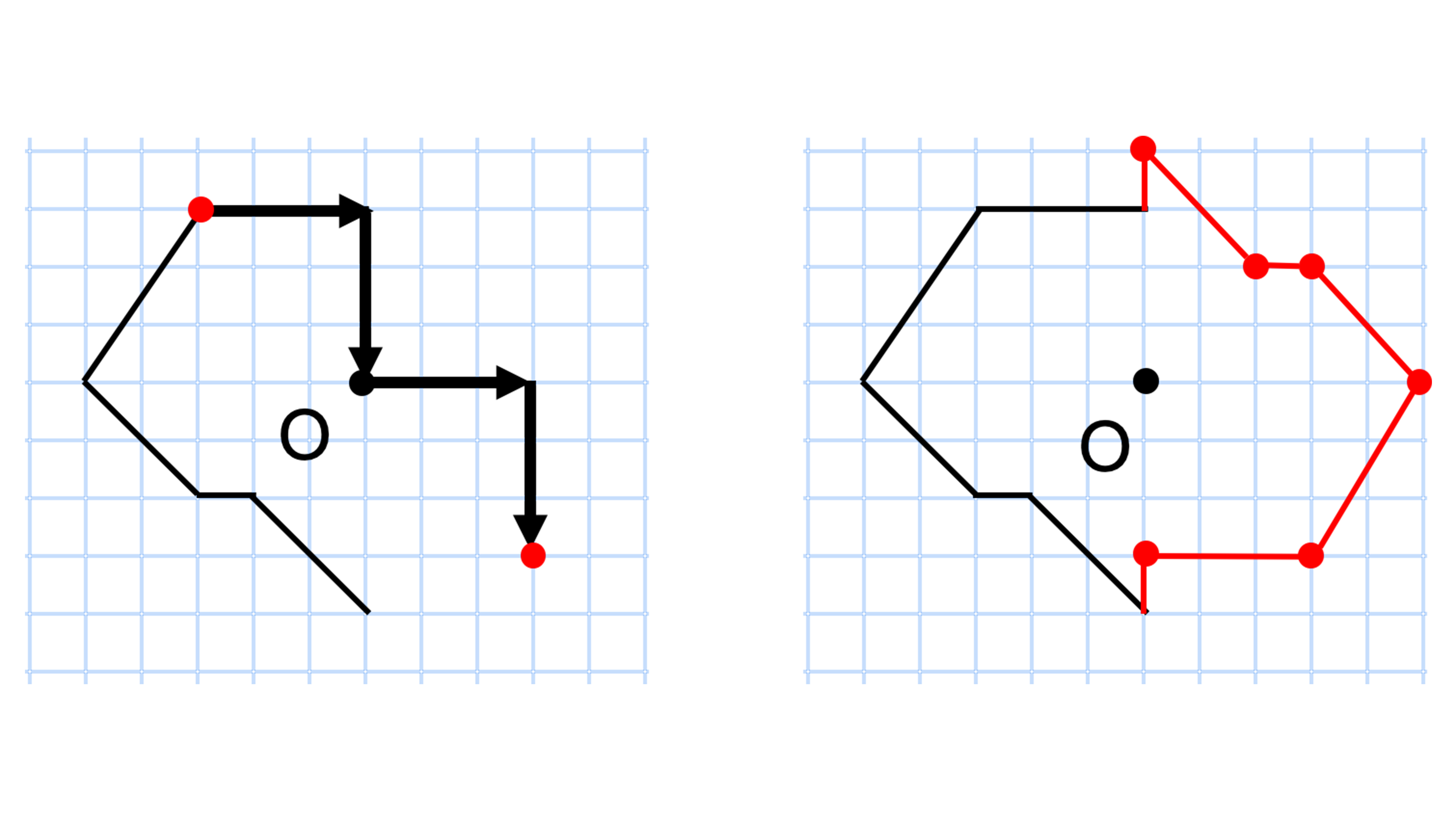
【作図方法②：マス目がない場合】
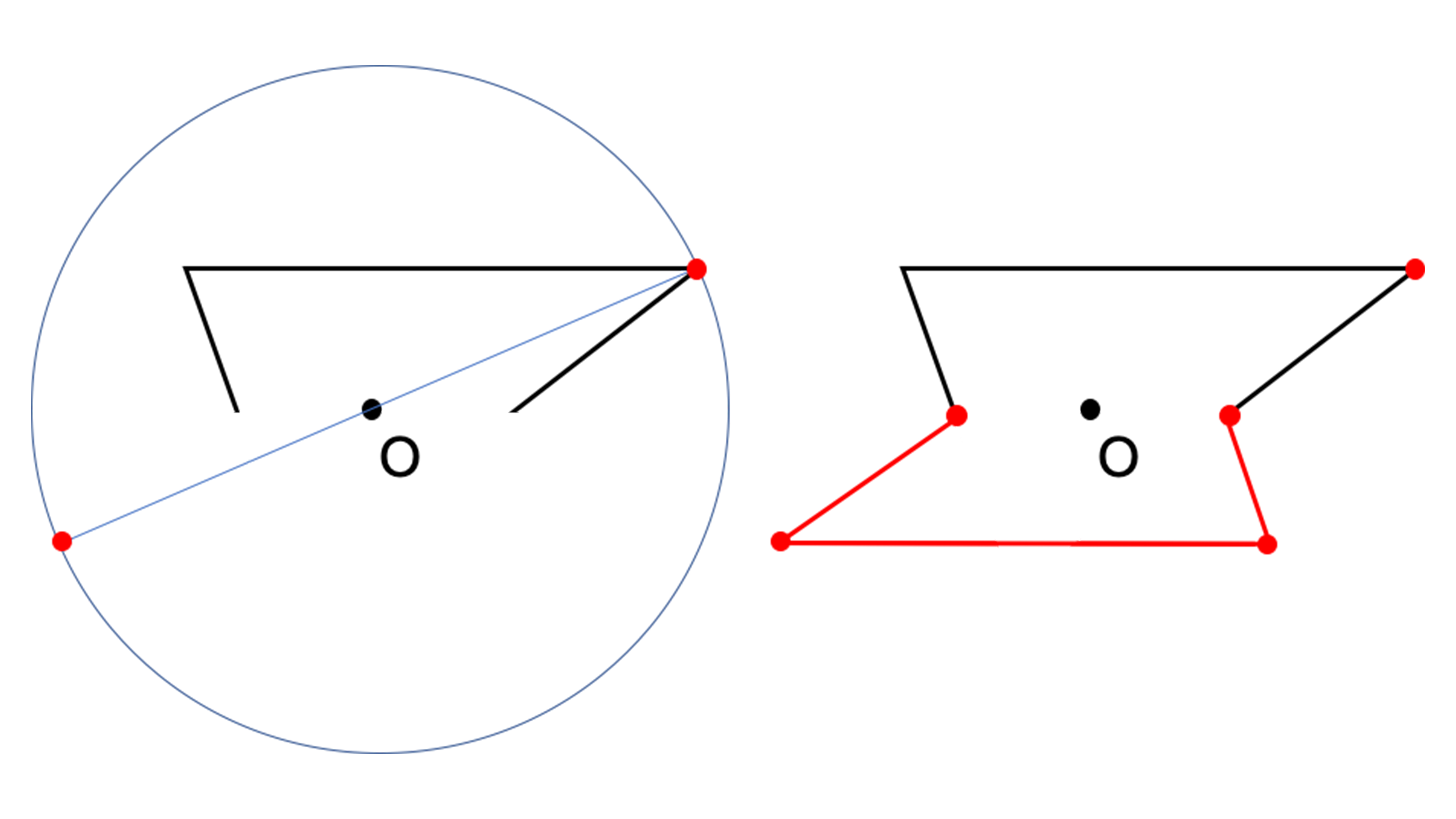
右側のようにマス目がない場合は、コンパスを使って作図しましょう。原点Oにコンパスの針を置き、図形の角(頂点)に鉛筆を合わせてください。そこから円を書きます。右上の角に鉛筆を合わせた場合、下の左図のような円が描けたでしょうか。そして、鉛筆を合わせた角から原点に向けて直線を引き、そのまま先ほど書いた円とも交差させてください。すると対応する点が定まりました。同様に他の点も対応する点を見つけ、つなぎ合わせると下の右図のような答えが導き出せます。

点対称な図形の練習問題にチャレンジ!!

基本情報が分かったら練習問題にチャレンジしましょう。解答は最後に載せてありますので、解き終えたら答え合わせをしてみてください。
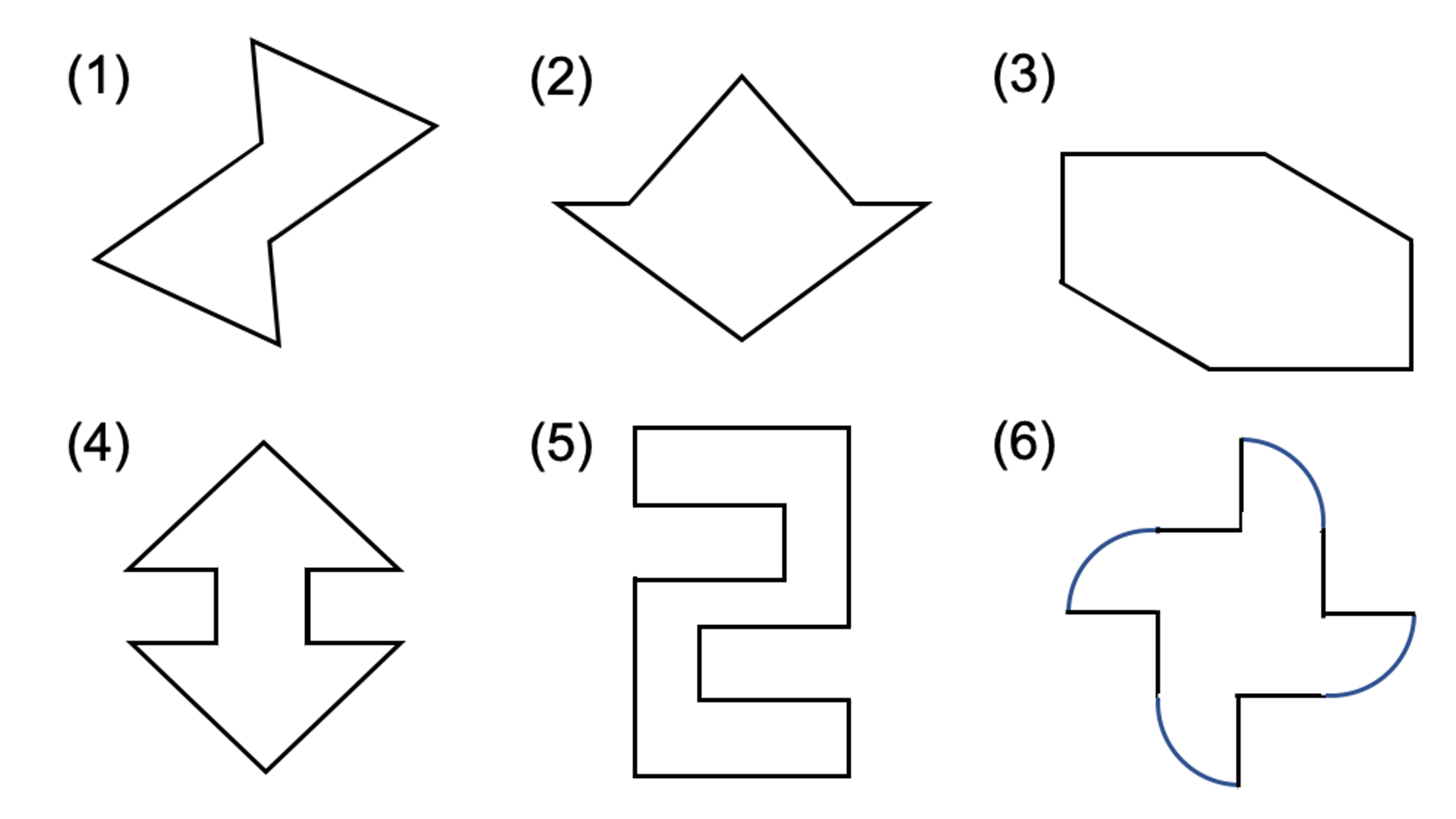
Q1 次の図で、点対称な図形には○、点対称な図形でないものには×と答えなさい。また、○をつけた図形には対称の中心Oをかき入れなさい。

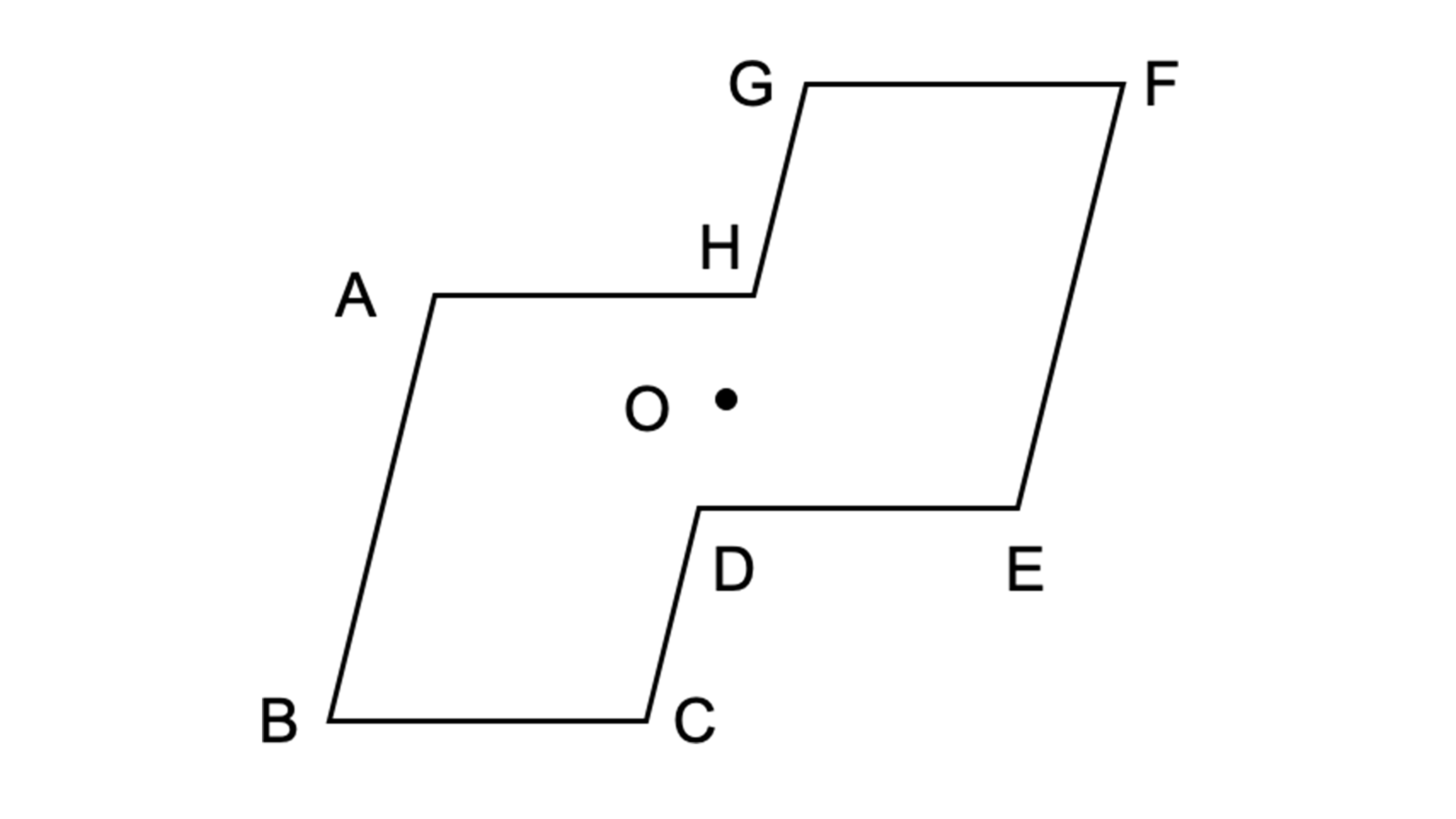
Q2 下の図は点対称な図形で、点Oは対称の中心です。
(1)頂点Aに対応する頂点はどれですか。
(2)辺CDに対応する辺はどれですか。
(3)角Bに対応する角はどれですか。

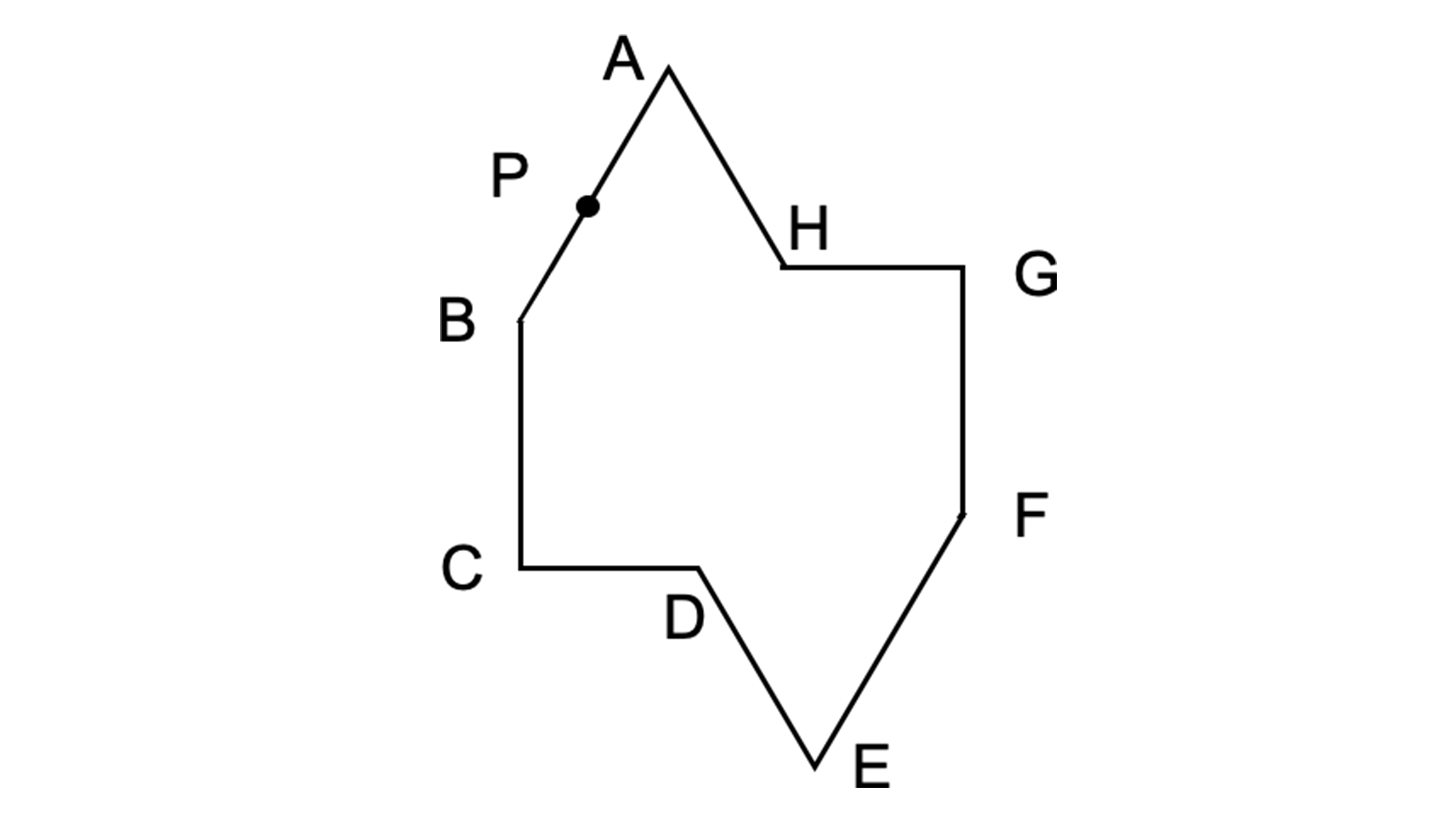
Q3 下の図は点対称な図形で、点Oは対称の中心です。
(1)点AとEを結ぶ直線は、どの点を通りますか。
(2)直線BOと直線FOの長さの関係はどうなっていますか。

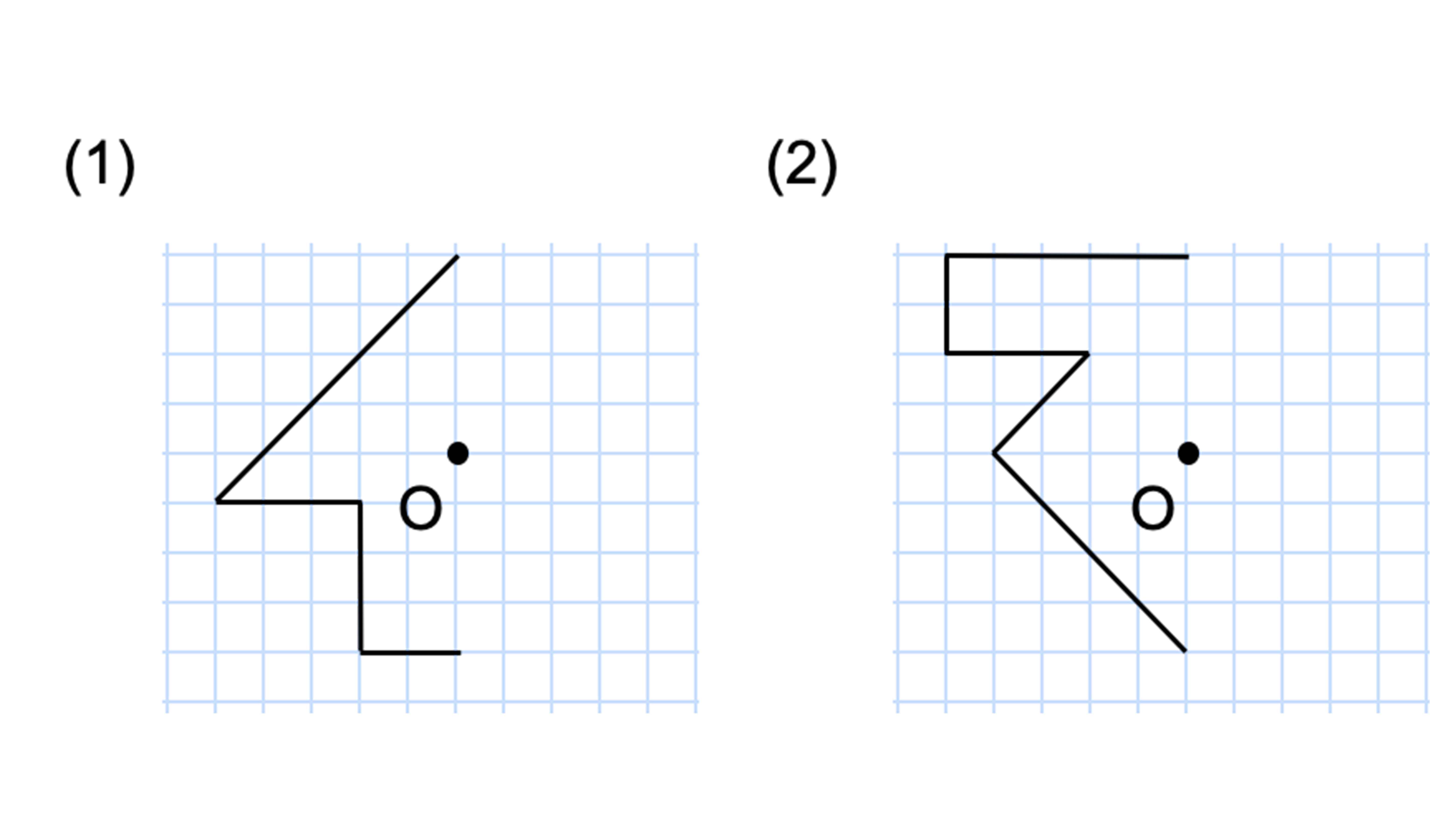
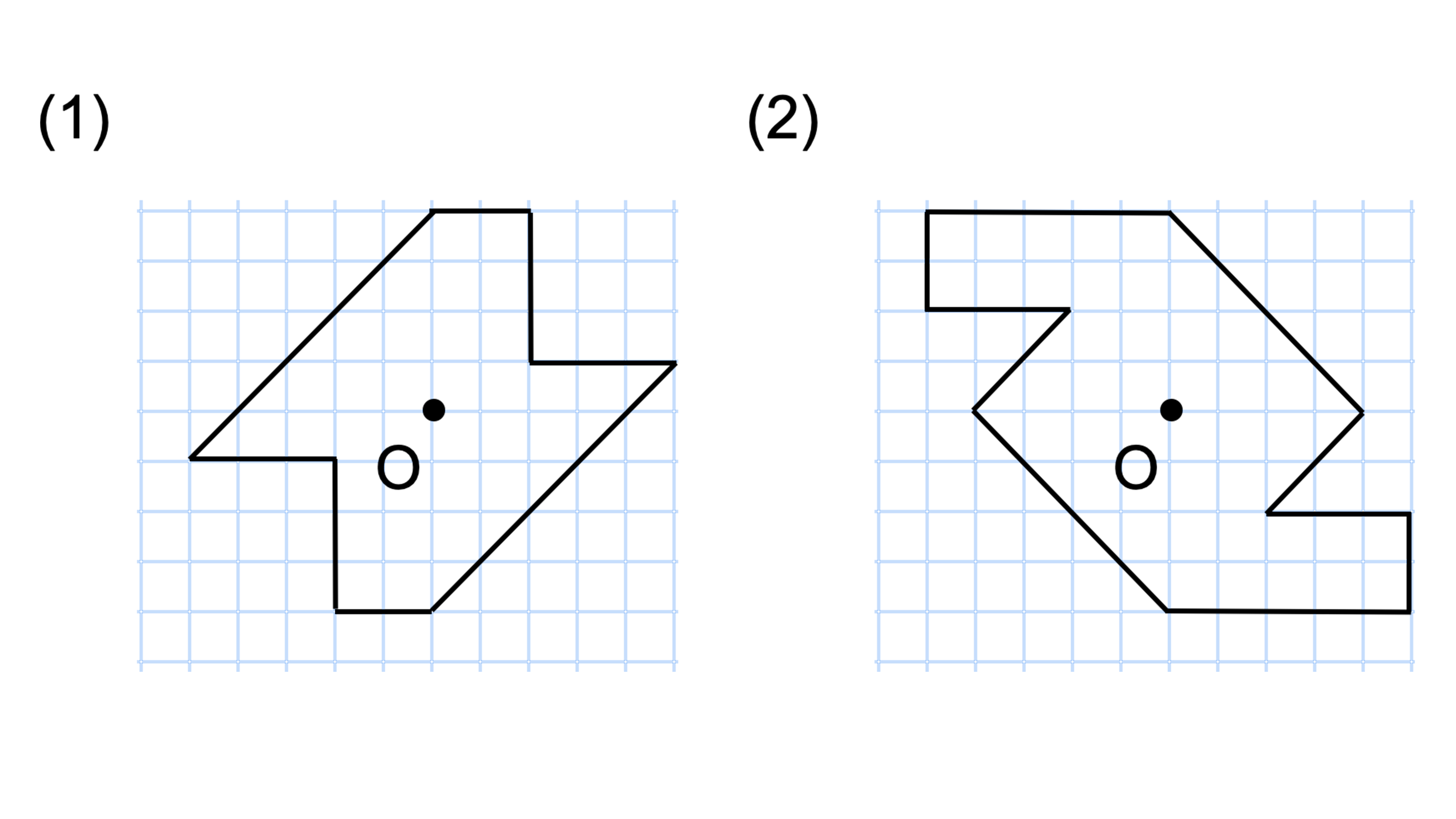
Q4点Oを対称の中心として、点対称な図形を書きなさい。

Q5 次の多角形について、点対称な図形には○、点対称な図形でないものには×と答えなさい。
(1)二等辺三角形
(2)正方形
(3)ひし形
(4)平行四辺形
(5)正五角形
(6)正八角形

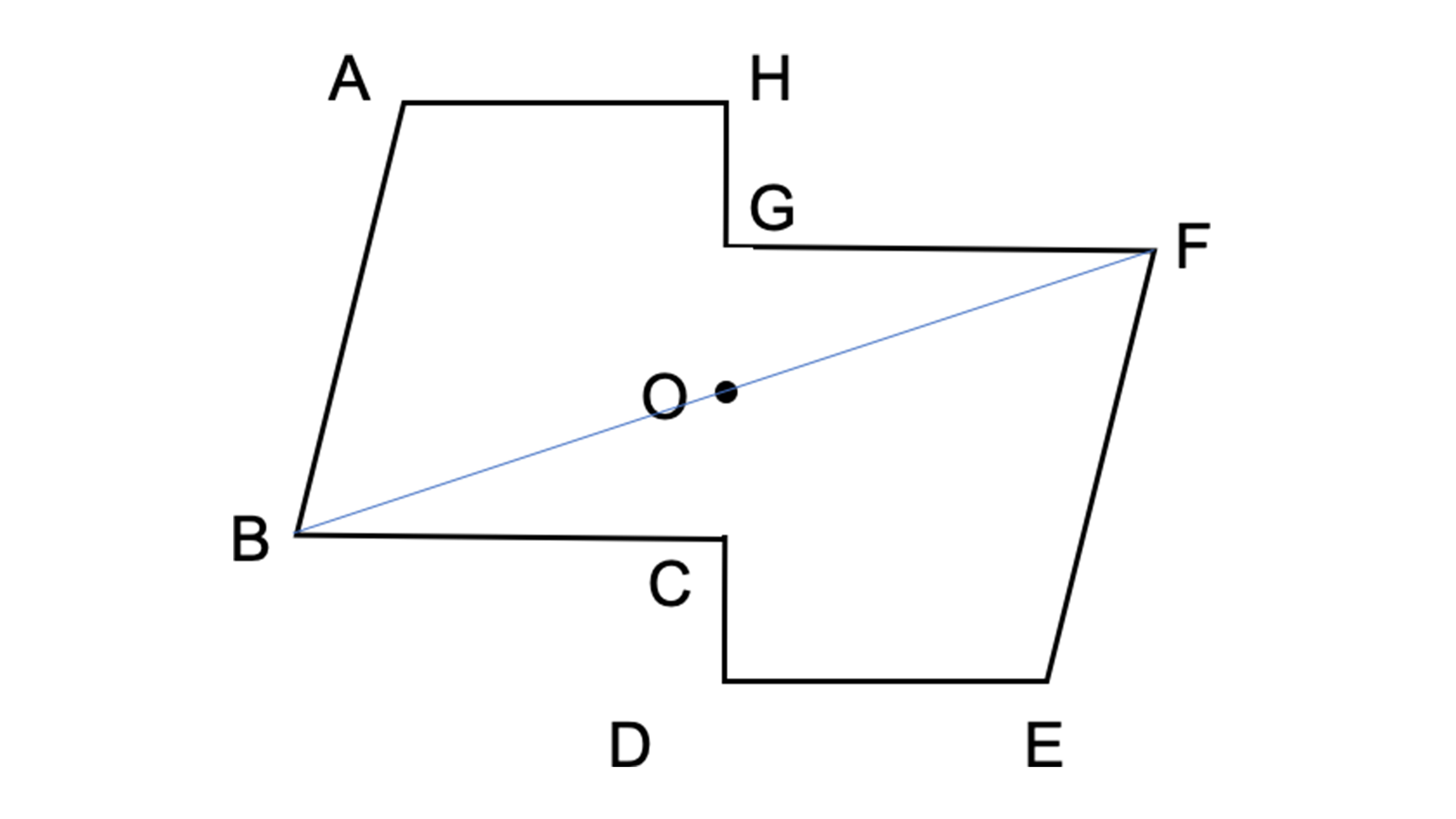
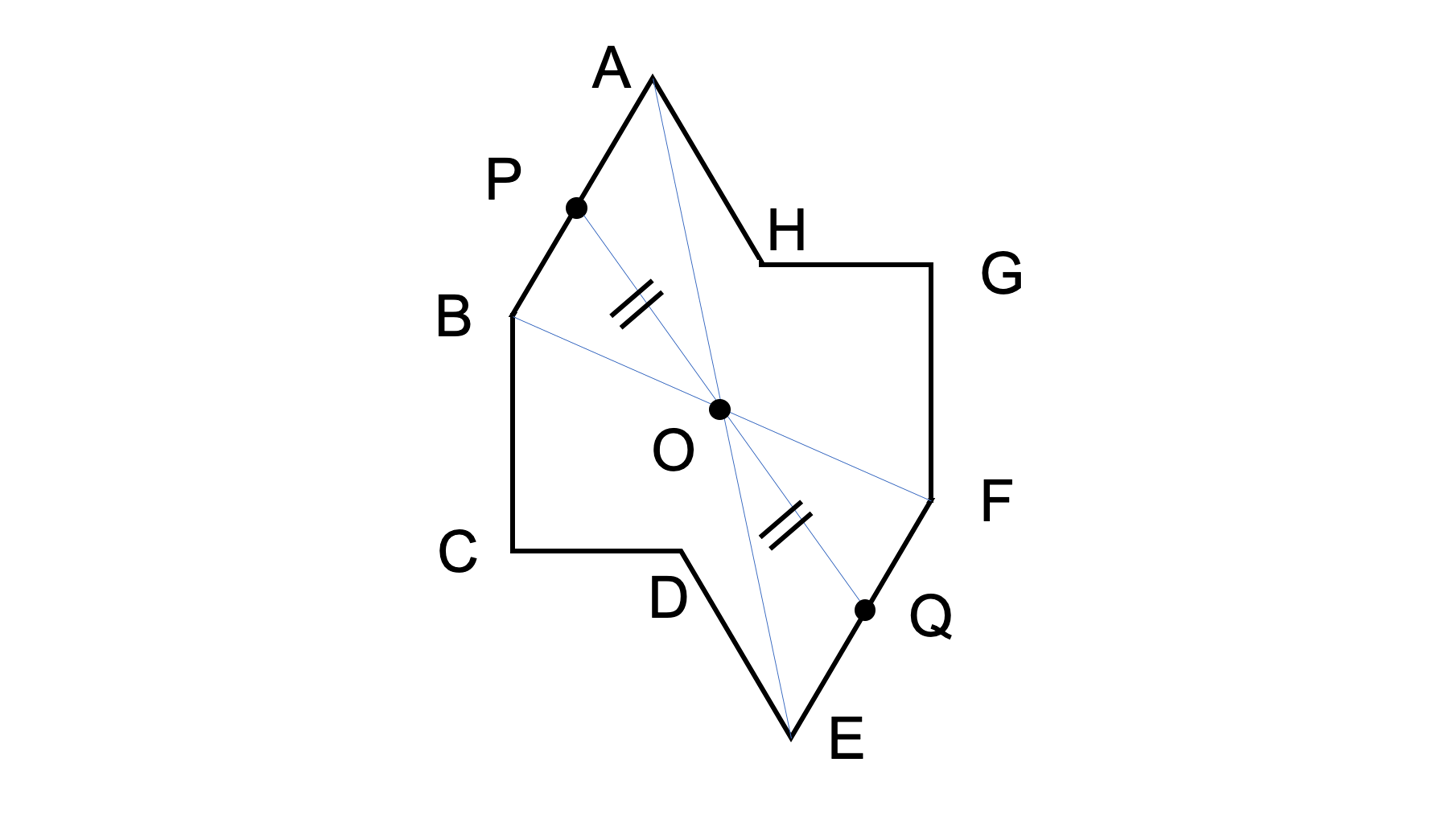
Q6下の図は点対称な図形です。
(1)次の点に対応する点はどれですか。
①点C ②点E
(2)次の辺に対応する辺はどれですか。
①辺AB　②辺GH
(3)次の角に対応する角はどれですか。
①角B ②角G
(4)点Pに対応する点Qを、図の中にかき入れなさい。

Q7 点Oを対称の中心として、点対称な図形をかきなさい。

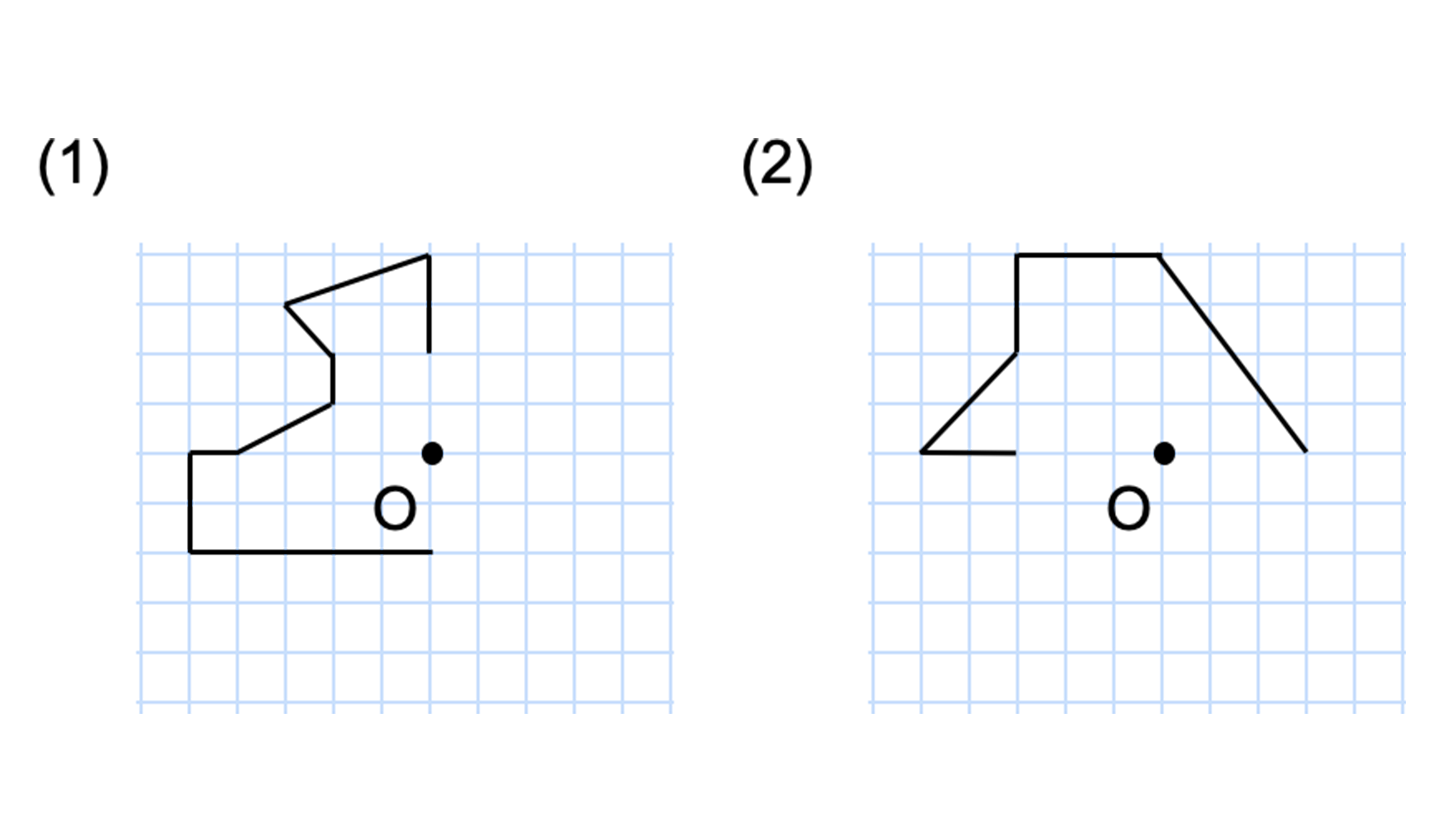
演習をつんで点対称を得意単元にしよう!!

点対称について基本から、間違えやすい線対称との違いを含めて今回はまとめました。ただ細かい計算が出てくる単元ではなく、暗記する情報も多くはないため、やれば得意な単元にできるかもしれません。多くの問題にチャレンジしてパターンに慣れていきましょう。

【練習問題の解答】

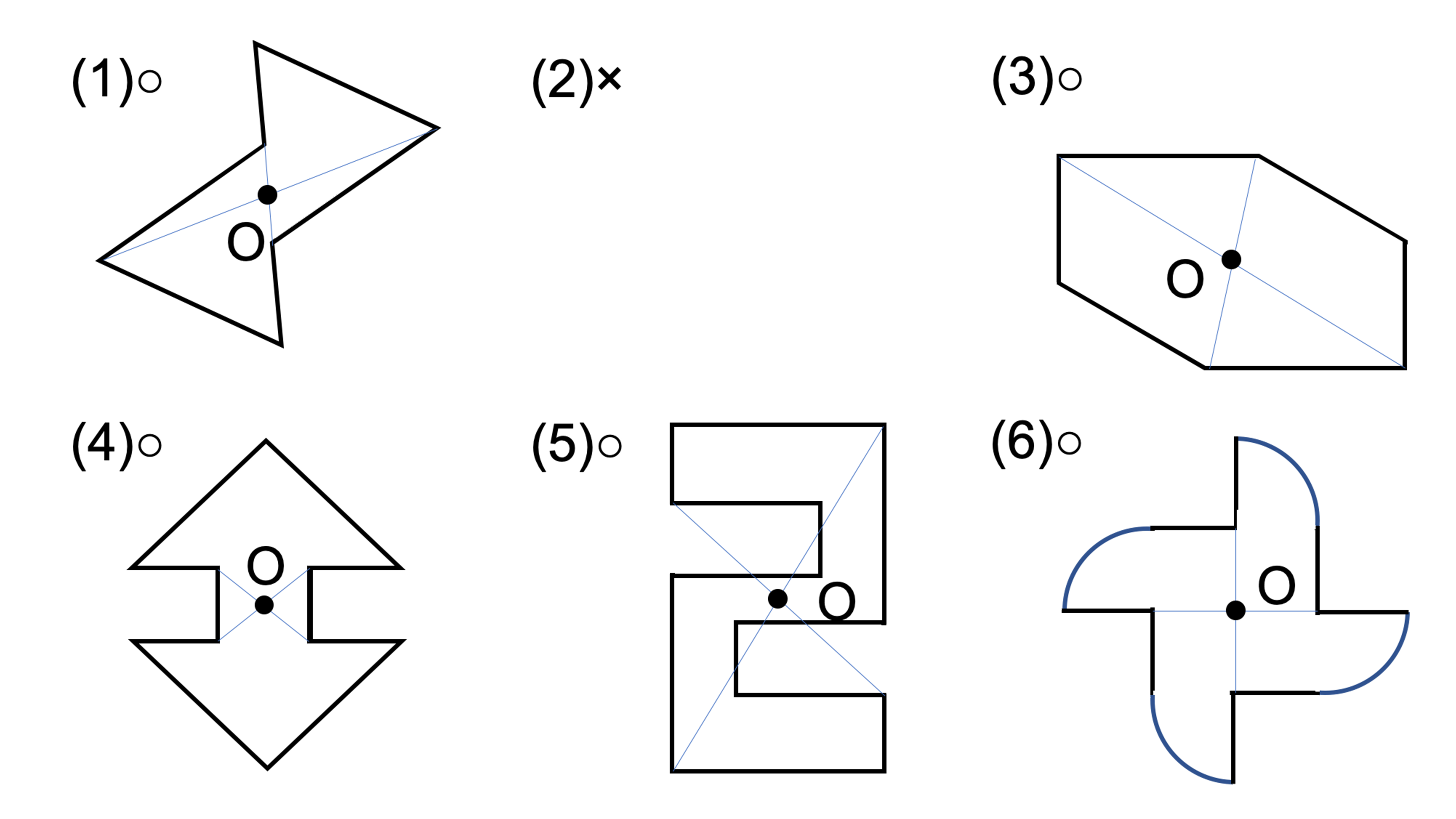
Q2 (1)頂点E (2)辺GH (3)角F
Q3 (1)点O (2)等しくなっている。
Q4

Q5 (1)× (2)◯ (3)◯ (4)◯ (5)× (6)◯
Q6 (1)①点G ②点A
(2) ①辺EF ②辺CD
(3) ①角F ②角C
(4)

Q7