｢素数｣とは？求め方や見分け方のコツ・法則を解説！

2・3・5・7・11……。これは｢素数｣の一例です。“1より大きい自然数のうち、1とその数でしか割り切れないもの”を素数と呼びます。しかし小学校5年生で習う内容なので、忘れている中学生がいるかもしれません。今回は素数の基本的な意味合いや用途をまとめました。まず一読して素数の情報を思い出しましょう。

素数とは、1より大きい自然数のうち、1とその数でしか割り切れないもの

素数とは、“1より大きい自然数のうち、1とその数でしか割り切れないもの”を指します。もっとも小さい素数は2で、1と2でしか2は割り切れません。1を除く自然数のうち素数でない最小の数は4です。4は2で割れる(4÷2=2)ため、素数の条件に合致しないのです。4のように、“自然数であり、1とその数以外の約数を持つもの”を｢合成数｣と呼びます。素数と区別するときに使いましょう。

また1を素数としないのには理由があります。たとえば4÷2=2と説明しましたが、1を入れてしまうと、4÷2÷1=2も成り立ってしまいます。さらに4÷2÷1÷1=2や4÷2÷1÷1÷1=2……とキリがありません。つまり1を素数としてしまうと都合が悪いのです。

くわえて素数には規則性がないといわれています。最小の2から順に数えていってもいつ素数が出てくるかが分かっていないのです。素数の数式化ができていないといってもいいでしょう。分かっていないからこそ『素数を数式化したい！』と考える数学者も多く、研究が盛んなテーマだといえます。

平方根や因数分解などで素数は使う

小学5年生の授業で素数を学習します。ただし実際の計算などで使用するのは中学で登場する｢因数分解(素因数分解)｣や｢平方根｣の単元が初めてかもしれません。それぞれ簡単に概要をまとめます。

因数分解(素因数分解)
因数分解とは、足し算・引き算の形の計算式や数字をかけ算の形に直す作業です。x^2+3x+2=(x+1)(x+2)のように、左辺では足し算の形になっている式を右辺でかけ算の形に変えます。とくに素因数分解の場合は、30＝2×3×5などと素数のかけ算の形に数字を整理する作業です。どれが素数か分かっていないとかけ算の形に整理できなくなります。

平方根
平方根とは、｢2乘すると◯になる値｣です。例として、9の平方根を求めてみましょう。つまり｢２乘すると9になる値｣を求めます。9は3か-3を2乘すれば得られるため、(±3)²=9が成り立ちます。ここで平方根をしめす記号の根号(√：ルート)を用いて左辺の2乘を省略しましょう。すると±3=√9と書けます。よって｢9の平方根(2乘すると9になる値：√9)が±3｣と求められました。｢2乘の逆｣や｢-2乘(マイナス2乘：x^-2=√x)｣などと説明される場合もありますが、シンプルに“2乘すると◯になる値”とまずは覚えてください。
また平方根のなかが2乘になると、根号の外に数字を出す必要があります。たとえば√12=√3×2²のため、2の2乘を根号の外に出して√12=√3×2²=2√3と整理するのです。2も3も素数であるように、根号のなかで素因数分解をするため、素数を覚えておく必要があります。

素数の見つけ方である｢エラトステネスのふるい｣とは？

中学校までの学習で登場する素数は100まででしょう。下の25個が該当します。

-----------------------------------
2・3・5・7・11・13・17・19・23・29・31・37・41・43・47・53・59・61・67・71・73・79・83・89・97
-----------------------------------

覚えるように先生から指示された人もいるかもしれません。覚えた方が、素数か合成数かの判断が素早くできるのは間違いないでしょう。もしくはその場で求めても問題ありません。素数の見つけ方の例を2つ紹介しますが、①はテストのときなどでも活用できるでしょう。

【素数を見つける方法①：消去法で倍数や偶数を削る】
◯一の位に着目
→0・2・4・6・8：偶数(2の倍数)のため除外
→5：5の倍数のため除外
◯各位の数字を足す
→和が3の倍数→3で割り決めるため除外
◯7で割る
　 →7で割れれば合成数、割りきれなければ素数
※100より大きい数字を素数か検討するときは、7以上の素数(11・13・17…)で数字を割って求めます。

【素数を見つける方法②：エラトステネスのふるい】
①と見分けるプロセスは似ていますが、具体的なリストに起こして視覚的に見やすくする方法があります。｢エラトステネスのふるい｣と呼ばれる方法です。実際にやってみましょう。

◯自然数のリストを用意する

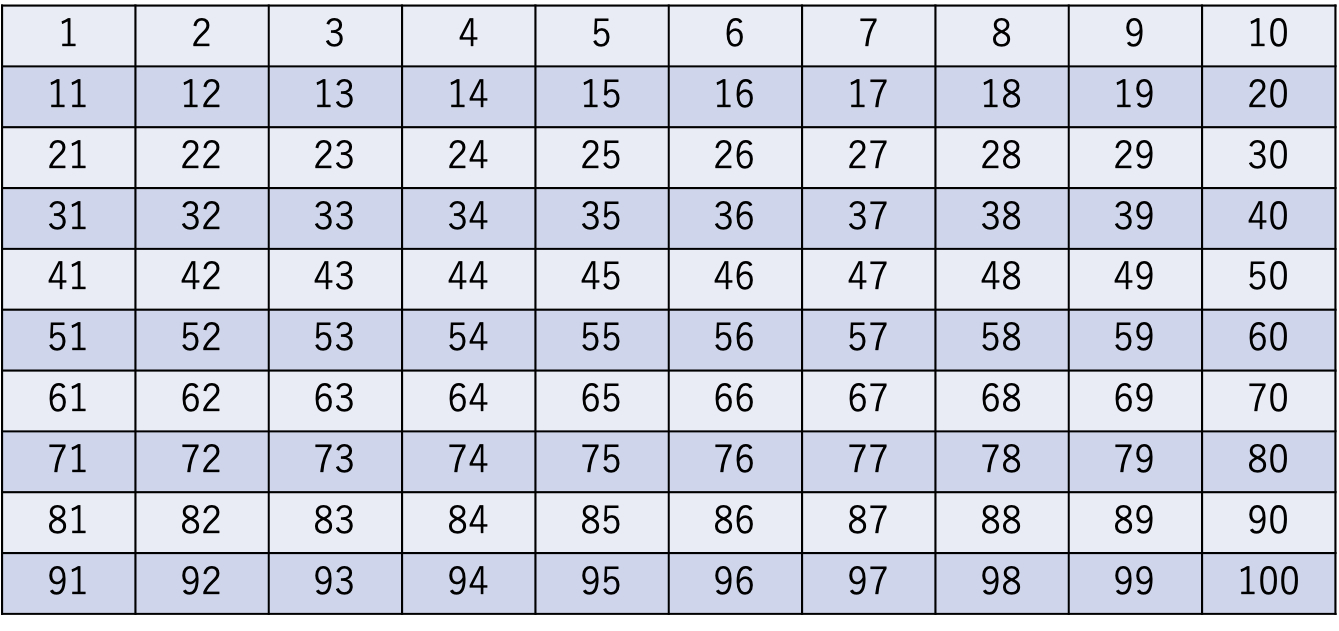
◯1は素数でないため除外

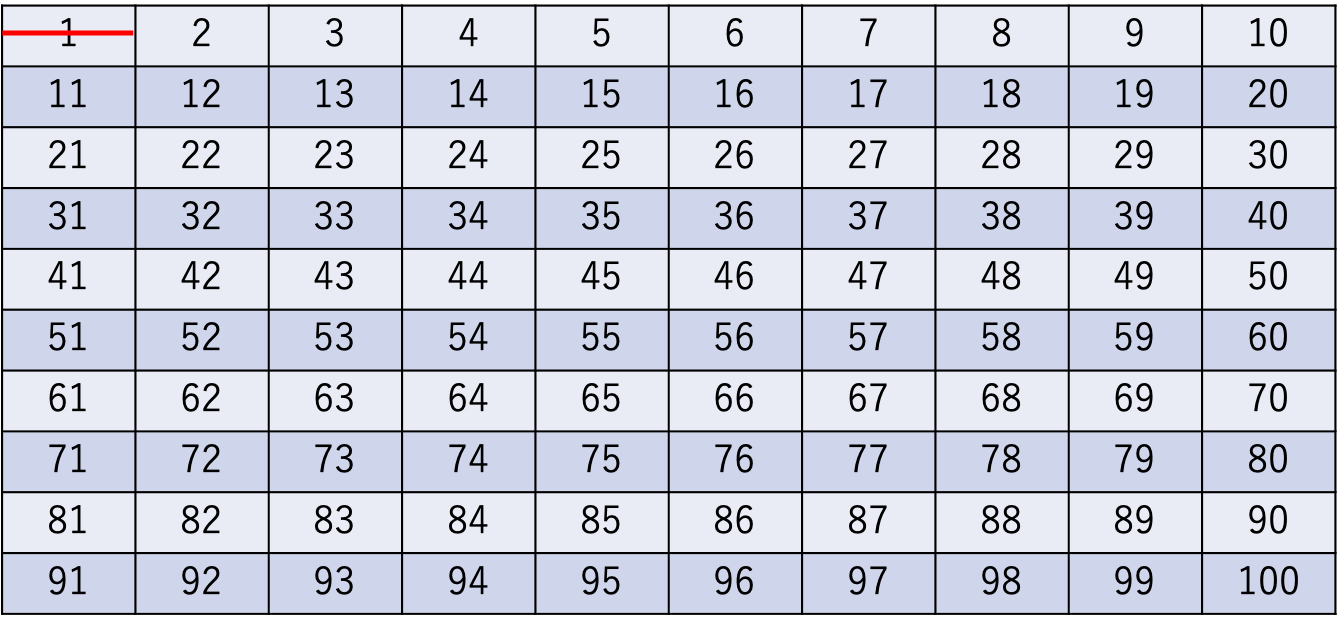
◯小さい方から素数の可能性を検討していく
→1の次にくる2を検討→2は素数
→2の倍数にあたる数字を消す
→偶数列が消える

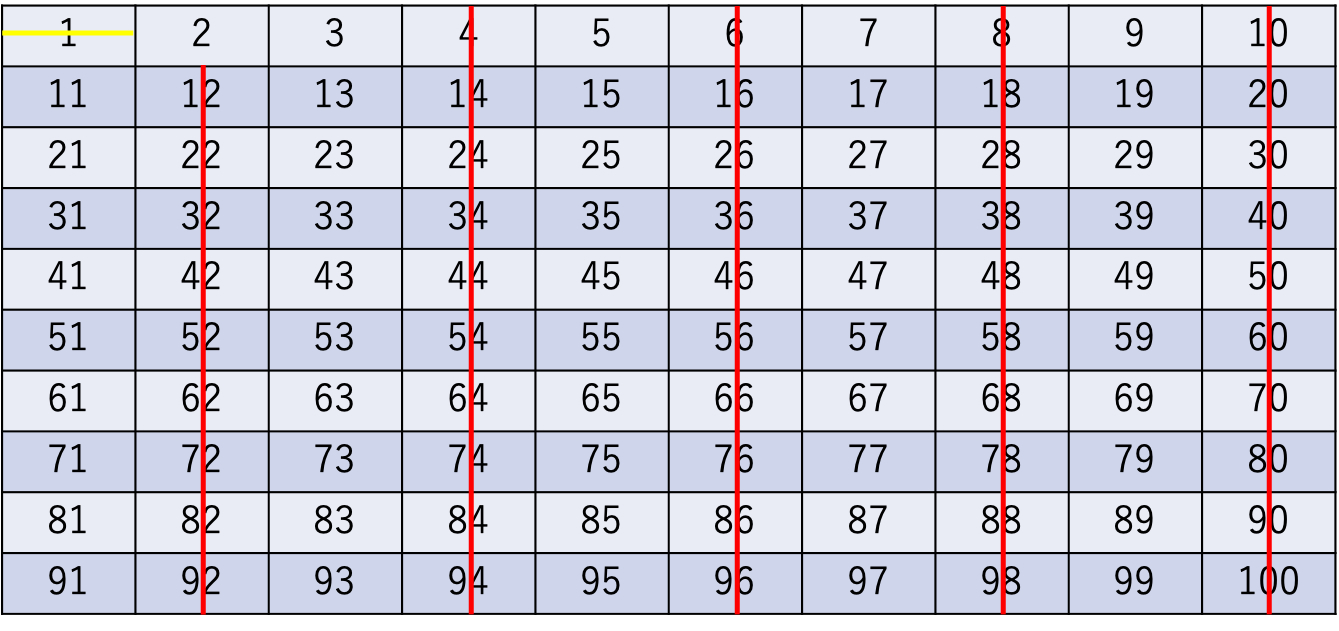
◯2の次に小さい数字を素数か検討する
→3を検討→3は素数
→3の倍数にあたる数字を消す
→斜めに線を入れて一気に消せる

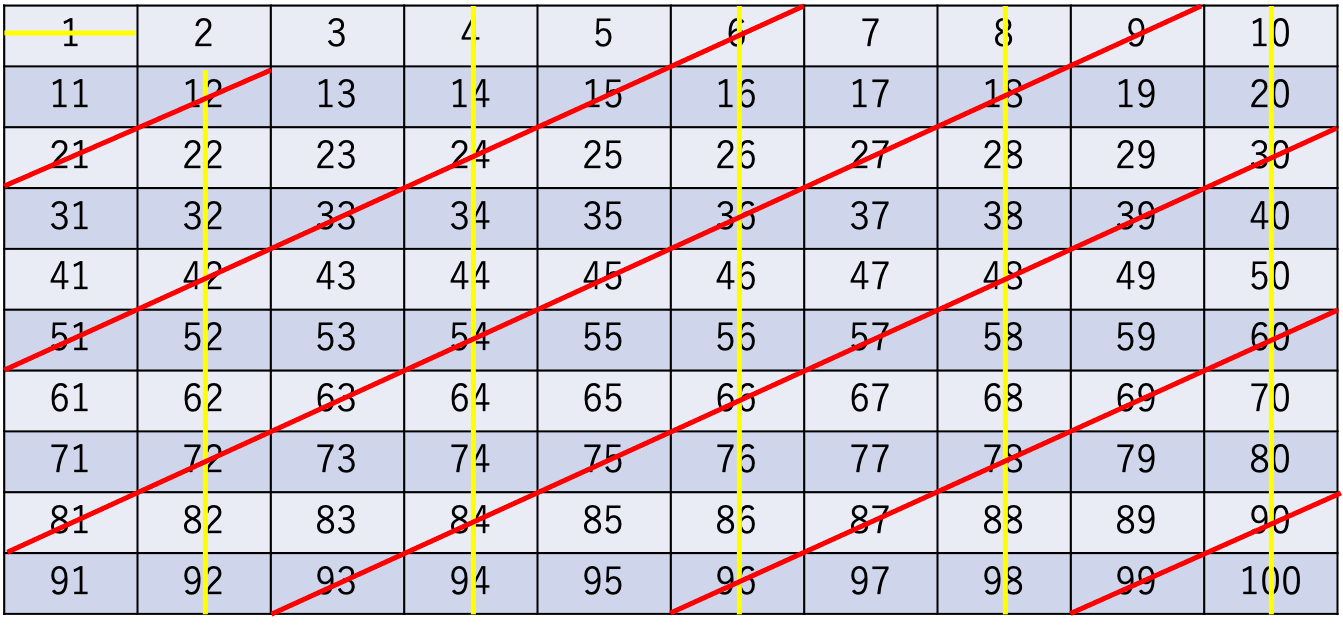
◯3の次に小さい数字を素数か検討する
→2の倍数である4はすでに消えている
→5を検討→5は素数
→5の倍数にあたる数字を消す(10の倍数は2の倍数なのですでに消えている)

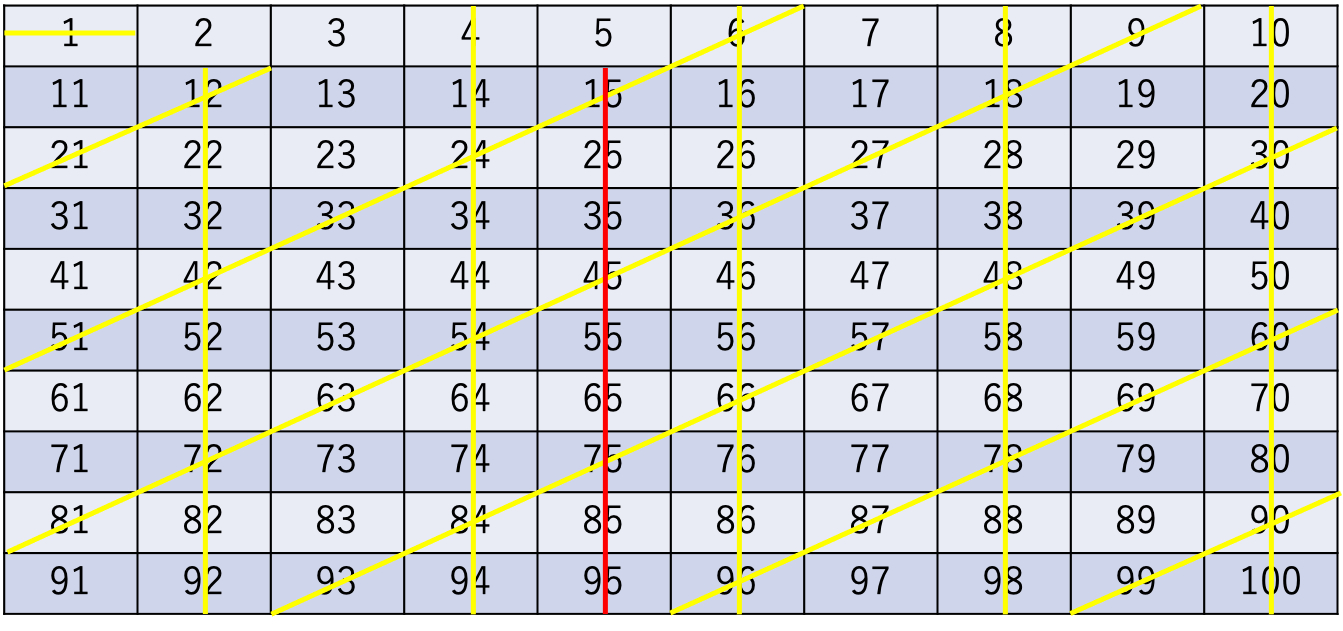
◯5の次に小さい数字を素数か検討する
→2・3の倍数である6はすでに消えている
→7を検討→7は素数
→7の倍数にあたる数字を消す(2・3・5の倍数に該当する7の倍数はすでに消えている)

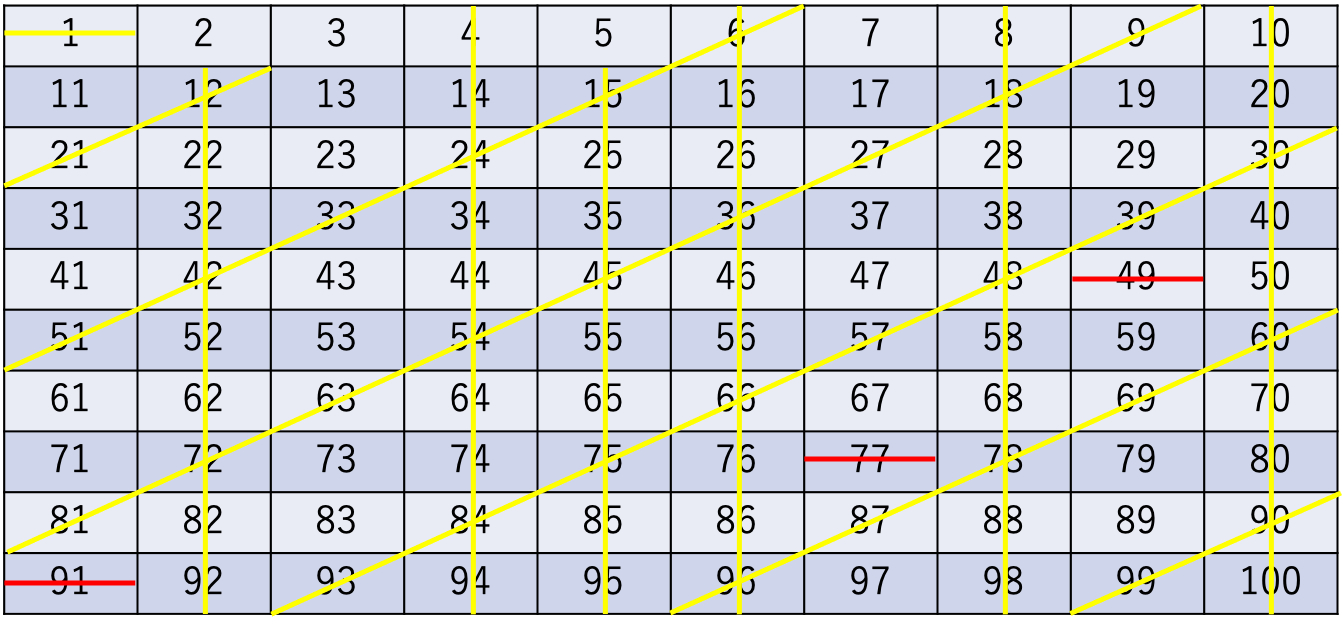
◯7の次に小さい数字を素数か検討する
→8・9ともすでに消えている
◯100は102のため、合成数の可能性を検討するのは9以下の数字同士の掛け合わせだけで十分(たとえば99＝9×11であれば、すでに9のときに検討済み)。
→残った数が素数(下の赤字)、消した数が合成数

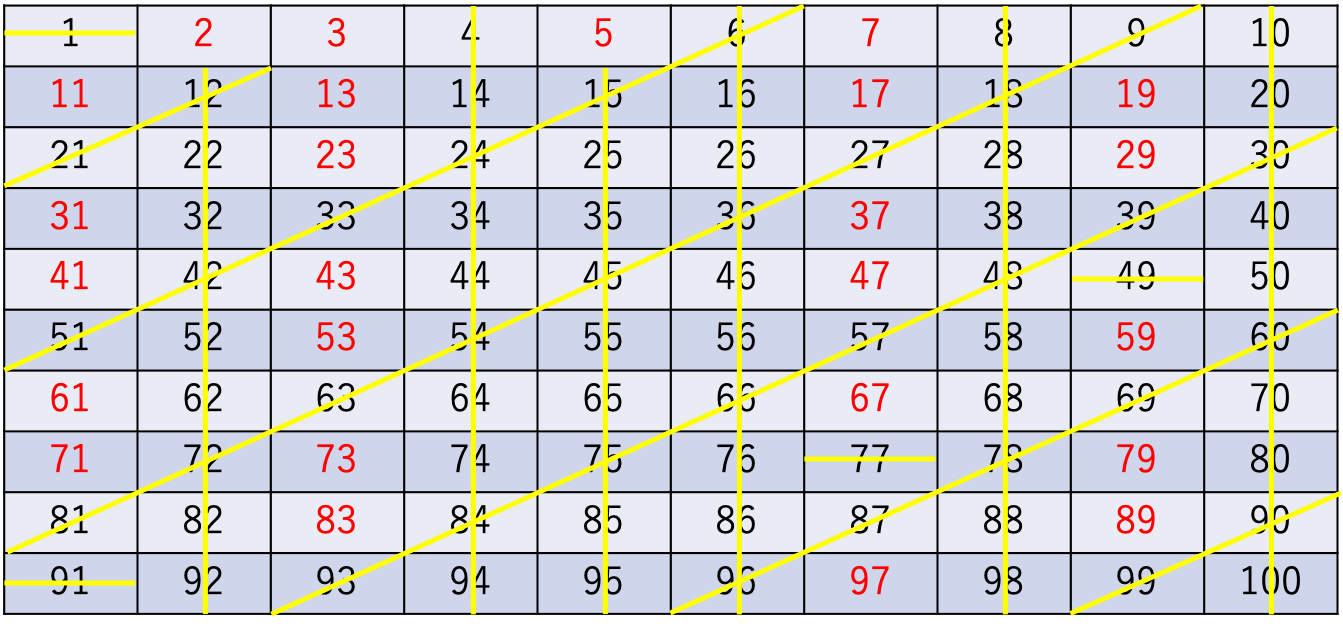
中学生なら問題にもチャレンジしてすぐに素数を復習！

あなたが小学5年生で初めて素数の説明を受けた段階ならまだ焦る必要はないでしょう。しかし素因数分解や平方根の説明をうけている中学生なのに『素数とは？』となっているならばすぐにでも復習をしてください。ひと通りの説明を今回まとめましたが、読んで分かったつもりで終わってはダメです。教科書や問題集の問題にもチャレンジして、素数をしっかりおさらいしましょう。