【中2数学】連立方程式とは？練習問題もご紹介

連立方程式は、多くの学生さんが苦手意識をもつ分野です。そもそも「連立方程式とは何か」がわからないまま授業が進み、クラスに置いていかれる方もいます。

この記事では、連立方程式とは何かや、代表的な解き方についてご紹介します。

＜この記事で紹介していること＞
・連立方程式とは
・解き方
・文章問題の考え方

連立方程式とは？

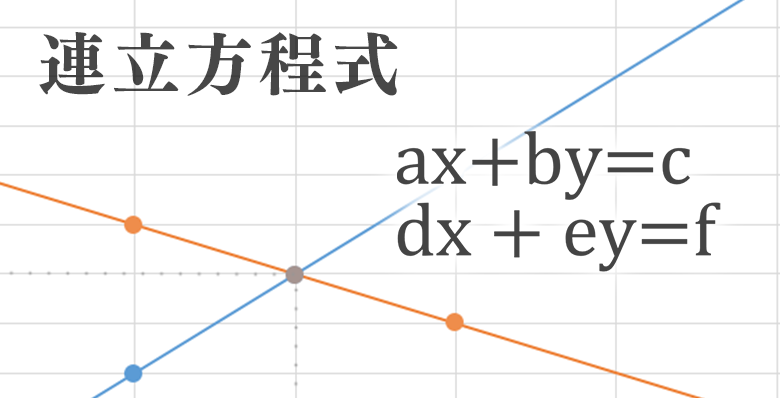
中学1年生で習う方程式では、1つの式に1つの文字が含まれます。一方、連立方程式には複数の文字が含まれます。連立方程式を解くには文字の種類と同じ数の方程式が必要です。

グラフにすると

連立方程式の例として「y=2x+1, y=-x+7」について考えてみましょう。グラフにすると以下のようになります。

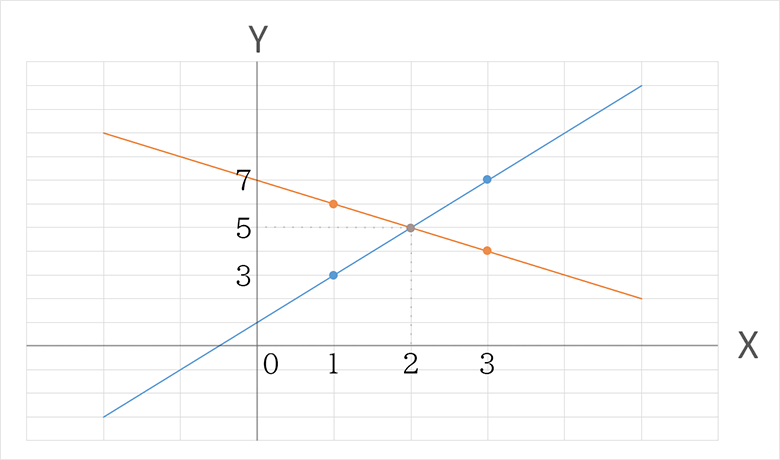
連立方程式を解くときの最終的な目標は2つの式を成り立たせるxとyの組み合わせを求めることです。

ここでグラフの交点(x=2, y=5)を見てみましょう。交点のxとyを2つの式に代入すると以下のようになります。

・x=2のときy=2x+1=2×2+1=5
・x=2のときy=-x+7=-2+7=5

ここから分かるとおり、連立方程式を解くときはグラフの交点を求めることをイメージするとよいでしょう。

連立方程式の解き方

連立方程式を解くために毎回グラフを描くと時間がかかってしまうでしょう。実は、連立方程式は式変形だけで解くことができます。

この記事では、代表的な解き方として「加減法」と「代入法」の2つをご紹介します。

加減法

加減法とは、式同士を足したり引いたりして求める文字を1つに絞る方法です。例として「2x-y=1, x+y=5」を縦に並べて考えてみましょう。

2x-y=1…①

x+y=5…②

①と②を縦同士で足す

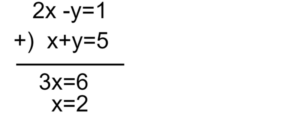
x=2を②に代入する

2+y=5

y=3

よって(x=2, y=3)と求まります。今回の問題のポイントは縦同士で足すときにyが消えるようにする点です。

問題によってはxが消えるように解く方が簡単な場合もあります。以下の練習問題で確かめてみましょう。

練習問題

以下の連立方程式を解いてみましょう。

x+2y=0…①

2x-3y=7…②

①の両辺に2をかけます。（左辺と右辺に同じ数をかけても式は成り立つ）

2x+4y=0…①’

2x-3y=7…②

①-②

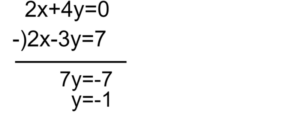
y=-1を①に代入します。

x-2=0

x=2

よって(x=2, y=-1)と求まります。

代入法

片方の式をもう片方の式に代入する方法を「代入法」と呼びます。「2x-y=1, x+y=5」を

例に考えてみましょう。

2x-y=1…①

x+y=5…②

②を「x=～」の形にします。

x=5-y…②’

②’を①に代入します。

2(5-y)-y=1

10-2y-y=1

-3y=-9

y=3

y=3を②’に代入します。

x=5-3=2

よって(x=2, y=3)と求まります。この問題では「x=～」の形の式を代入しましたが「y=～」を代入して解くこともできます。以下の練習問題で確かめてみましょう。

練習問題

以下の連立方程式を解いてみましょう。

2x+y=0…①

-3x+2y=7…②

①を「y=～」の形にします。

y=-2x…①’

①’を②に代入します。

-3x+2(-2x)=7

-7x=7

x=-1

x=-1を①’に代入します。

y=-2(-1)

y=2

よって(x=-1, y=2)と求まります。

文章問題の解き方

連立方程式の文章問題では「どの数量を文字で表すか」を決める必要があります。基本的には、求める数量を文字にします。例題で考えてみましょう。

例題

ある遊園地の入場料は、大人2人と子ども2人で4000円、大人1人と子ども3人で3600円です。大人1人と子ども1人の入場料をそれぞれ求めましょう。

解答

求める数量は「大人1人の入場料」と「子ども1人の入場料」の2つです。大人の料金をx円、子どもの料金をy円として解きましょう。連立方程式をたてると以下のようになります。

2x+2y=4000…①

x+3y=3600…②

加減法で解くために①-2×②でxを求めます。

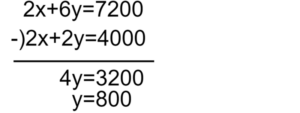
y=800を②に代入します。

x+2400=3600

x=1200

よって、大人1人が1200円、子ども1人が800円とわかります。

練習問題

問題①

あるお店でみかんとりんごを1個ずつ購入すると定価で500円かかります。

ところが、お店に立ち寄った日は特売日で、みかんが2割り引き、りんごが4割り引きで売られていたため、代金の合計は357円になりました。

みかんとりんごそれぞれの値段を求めましょう。

解答①

みかん1個をx円、りんご1個をy円とします。すると、以下の式が成り立ちます。

x+y=500…①

0.8x+0.6y=357…②

①×4-②×5をします。

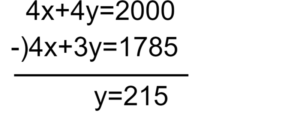
y=215を①に代入します。

x+215=500

x=285

よって、みかん1個285円、りんご1個215円とわかります。参考までに、この問題をグラフにすると以下のようになります。

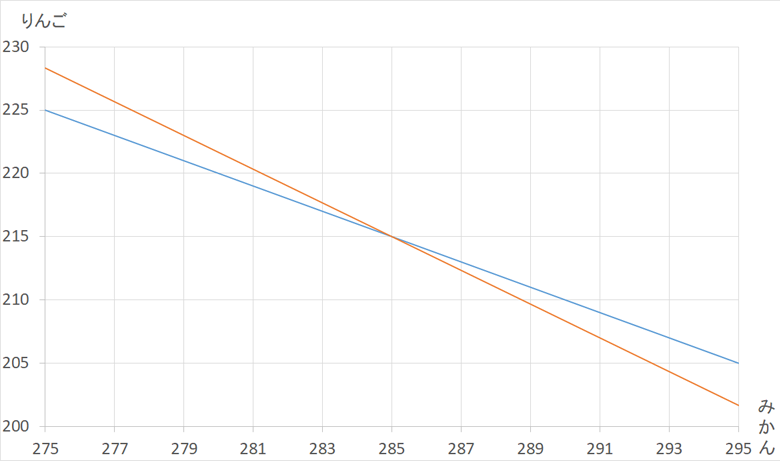
問題②

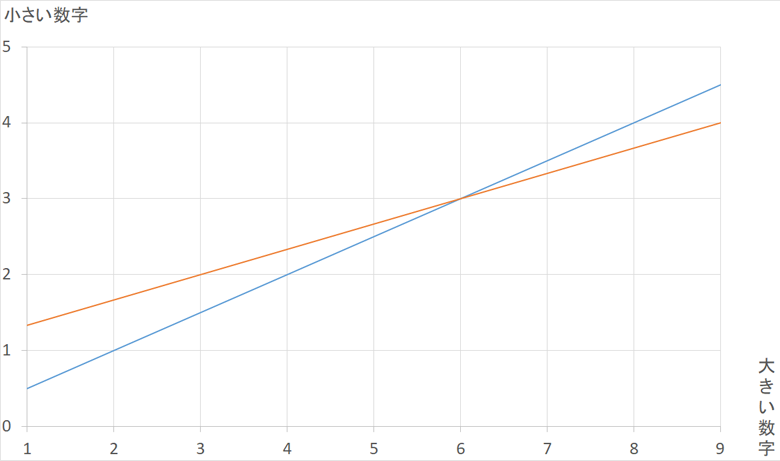
大小2つの数字があります。大きい数字は小さい数字の3倍よりも3小さい数字です。小さい数字は大きい数字の半分です。2つの数字を求めましょう。

解答②

大きい数字をx、小さい数字をyと考えると以下の式が成り立ちます。

x=3y-3…①

y=0.5x…②

①を②に代入して代入法で解きます。

y=0.5(3y-3)…②’

②’の両辺を2倍します。

2y=3y-3

y=3

y=3を①に代入します。

x=3×3-3

x=6

よって(x=6, y=3)と求められます。参考までに、この問題をグラフにすると以下のようになります。

数学が苦手な人は『個別指導塾スタンダード』がおすすめ

連立方程式には複数の式や文字が出てくるため、苦手意識を感じる学生さんが多くいらっしゃいます。

式同士のひっ算や複雑な式変形などで苦戦する方も多いでしょう。

勉強の効率を上げるためには、分からない問題をすぐに誰かに聞ける環境が必要です。少しでも数学に苦手意識を感じるのであれば、塾に通いながらの勉強がおすすめです。

わからないポイントを一つひとつ解決し、応用問題でも解けるようにサポートを受けられます。

『個別指導塾スタンダード』では、オーダーメイドのカリキュラムと呼ばれる自由度の高い学習環境を提供しています。

生徒のみなさん一人ひとりに合わせた指導をおこなっているため、自分のペースで学習を進められるでしょう。

無料体験授業も実施しているため、ぜひ下のリンクからお近くの教室を確認してみてください。

近くの教室をチェックしてみる

連立方程式は繰り返し解こう

連立方程式の文章問題では、xとyを何にするのかを自分で決めなければなりません。最初は慣れないかもしれませんが、何度も解くことでxとyの決め方がわかるようになります。

テストで高得点を取るためにも、連立方程式の解き方が定着するまで繰り返し問題を解くようにしましょう。

『個別指導塾スタンダード』では無料体験授業を実施しています。下のリンクから近くの教室をチェックできるため、気軽にお試しください。

近くの教室をチェックしてみる