個別指導塾スタンダードのお役立ち情報
1つずつ丁寧に計算すれば解ける!「円柱」の体積・表面積の求め方
図形問題は得意ですか? 考え方がよくわかっていなかったのに「公式もしっかり覚えるように」と言われて学校の授業は終わってしまった……と困っている人もいるかもしれません。
そんな図形の中から中学一年生で登場する「円柱」の体積と表面積についてまとめました。公式も紹介していますが、計算する流れをしっかり理解して頭に入れましょう。
「円柱」とは底が円で筒の形をした図形

底が円の形をした筒状の図形を「円柱」と呼びます。天面(上の底)と底面(下の底)が同じ円形をしている立体といってもいいかもしれません。たとえば上の左のような図形を指します。
似たような言葉で「円錐」があります。上の右の図形のように、円柱と同じく底面は円形をしていますが、円錐は底面から上にかけてとがった形をしています。真上から見たら円柱と同じ形に見えますが、真横から見たら三角形に見える、トゲのような形です。
円柱の体積の求め方=半径×半径×円周率×高さ

円柱に関して、体積を求める問題がよく作られます。たとえば上の写真のように、底の円の半径と円柱の高さが示されて「この円柱の体積を求めよ」と問われます。
上の情報を元に計算の流れを説明していきましょう。まずは底面積(S)を求めます。「底面積=半径×半径×円周率」で計算できるので「6×6×π=36π(cm2)」が底面積です。そして、底面積×高さ(h)=円柱の体積ですから、「36π×13=468π(cm3)」が答えです。これを公式化すると下のようになります。
---【公式】---
円柱の体積=底面積×高さ
=半径×半径×円周率×高さ
=πr2h
=Sh
-----------------
ちなみに円錐の体積を求める公式もあります。詳しくは別の機会に説明できればと思いますが、円錐の体積は底面が同じ形の円柱の1/3になります。公式化すると下のようになります。
---【公式】---
円錐の体積=底面積×高さ×1/3
=半径×半径×円周率×高さ×1/3
=1/3πr2h
=1/3Sh
-----------------
【練習問題】
(A)下の円柱の体積をリットルで答えよ。 ※回答例は記事の最後をチェック

円柱の表面積は展開して求めてみよう

体積と同じく、円柱に関して問われるのが「表面積」です。体積と同じく、「この円柱の表面積を求めよ」と問われるのですが、円柱を展開して考えると分かりやすいです。体積の説明で使用したのと同じ、半径6cm・高さ13cmの円柱ですが、展開すると上の図のようになります。
まずは、底面の円周を求めます。円周は「直径×円周率」で計算できるので「2×6×π=12π(cm)」になります。続いては展開すると四角形に見えますが、側面積を求めましょう。四角形と同じく「縦×横」で計算でき、縦は与えられた13cm、横は先に求めた底面の円周と等しいので12π。2つを掛け合わすと「13×12=156π(cm2)」になります。
底面積・天面積は「半径×半径×円周率」で計算できるので「6×6×π=36π(cm2)」です。最後に、求めてきた2つある円(底面・天面)と四角形(側面)の面積を足し合わせると表面積が求められます。
表面積=側面関+底面積+天面積
=156π+36π+36π
=228π(cm2)
---【公式】---
円柱の表面積=底面積×2+側面積
=2×円周率×半径×(高さ+半径)
=2πr(h+r)
=2πrh+2πr2
-----------------
【練習問題】円柱の表面積を計算してみよう
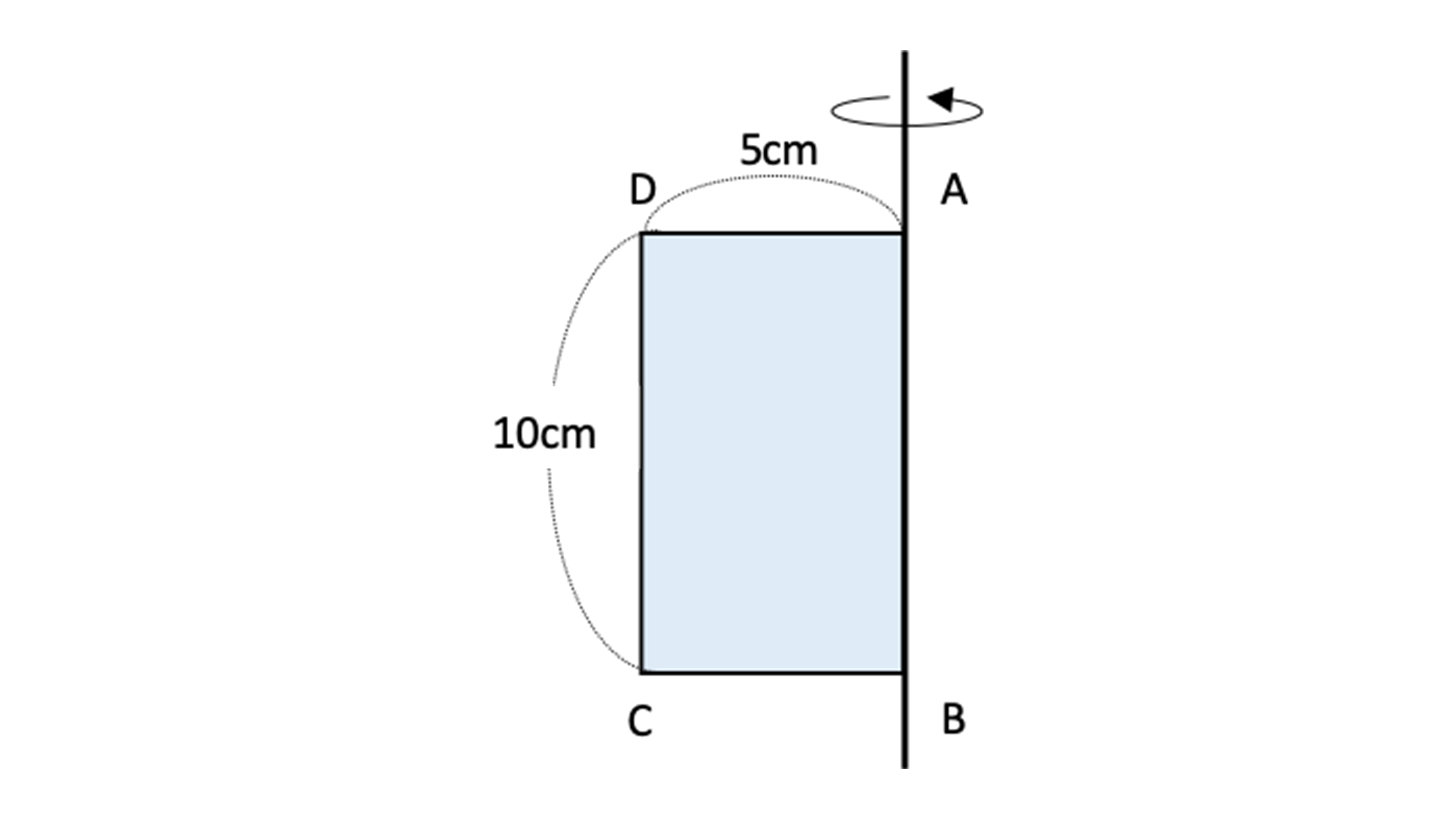
(B) 上図の長方形ABCDを直線ABを軸に1回転してできる立体の表面積を求めよ。
【練習問題回答例】
(A)図より、底面の円の半径=18/2=9cm
底面積(S)=9×9×π=81π(〖cm〗^2)
高さ=15cmより、体積=81π×15=1215π(cm3)
答え:1.215ℓ
※与えられているのが、半径でなく、直径であるのに注意
※1000cm3=1ℓ
(B)長方形ABCDを一回転させてできる円柱と、それを展開した図は下の通りになります。
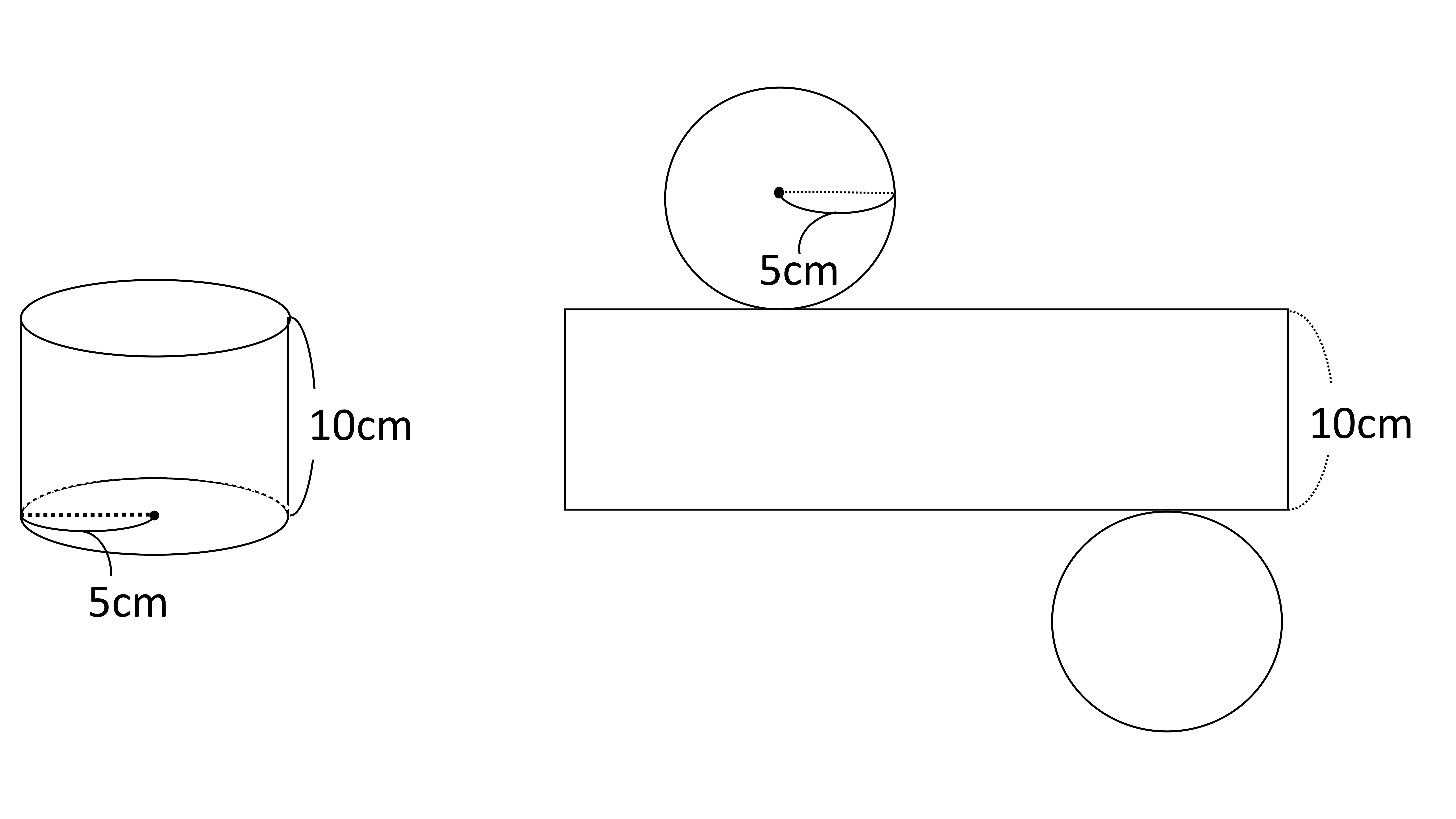
底面積・天面積=5×5×π=25π
側面積=(5×2×π)×10=100π
表面積=底面積+天面積+側面積=25π+25π+100π=150π
答え:150πcm2
公式を忘れても、円柱に関する問題はひとつずつやれば解ける

練習問題(B)は応用的な内容でしたが、正解できましたか? 公式を当てはめて問題を解くのはもちろん、テストや入試など緊張する場面で公式が思い出せないときは半径・直径や高さになる数字を冷静に確認してみてください。ひとつずつ丁寧に計算してみればきっと正解にたどりつけるでしょう。