「表面積」の求め方まとめ！立体ごとの違いやポイントをチェック

図形の問題で外せないのが「表面積」の計算です。立体の種類に合わせて計算方法を変えなければなりませんが、全部理解できているでしょうか。今回は立体の種類に合わせて、表面積の計算の流れをまとめてみました。4つのポイントを意識しながらチェックしてみましょう。

立体の表面積を求め方

表面積とは、立体を形成する全ての面の面積を合計した値です。地面と接している底面も含む、立体が空気に触れている外側の面の面積を全て足した値や、立体を展開してできる「展開図」の面積の値など色々な言い方がされます。紙を切り貼りして立体を作るときに必要な紙の面積の合計といってもいいでしょう。

表面積を求めるときには、底面の面積である「底面積」と側面の面積である「側面積」をそれぞれ計算して足し合わせるのが一般的です。つまり「底面積＋側面積＝表面積」が基本といえます。

ただし三角形・四角形・円など底面の形が違っている点にまず注意しなければなりません。さらに立体にしたときに柱や棒のように太さが一定の「柱体」のときもあれば、上にいくにつれて太さが変わって尖った針のようになる「錐体」のときもあります。とくに柱体の場合は、底面と合同な面が下だけでなく上にもついている(上面)ため、底面積を2つ分とらなければなりません。つまり底面の形や立体の太さ(形状)を見分けながら計算方法を変えなければならないのです。

立体の種類別で表面積の求め方をチェック

立体の種類ごとに計算の仕方をそれぞれ確認していきましょう。底面の形や立体にしたときの太さで名前も変わっています。もちろん公式として覚えても良いので、特徴をしっかり理解していきましょう。

「角柱」の表面積

太さが一定で“◯◯柱”と呼ばれる「柱体」から表面積の求め方をチェックしていきましょう。まずは底面が多角形の場合です。底面が多角形で、太さが一定の立体を「角柱(かくちゅう)」と呼びます。底面が三角形であれば“三角柱”・四角形であれば“四角柱”と呼び方が変わるのでした。角柱の表面積を求めるときのポイントは下の4つが挙げられます。
[1]底面の形に合わせて計算方法が変わる点
[2]底面と合同な上面もあるため底面積を×2にする点
[3]側面を展開したときには四角形(長方形)になる点
[4]底面の全ての辺の長さの合計と立体の高さを掛け合わせて側面積を求める点
三角柱の場合をチェックしてみましょう。

＊底面積＊
底面は三角形 → 三角形の面積＝縦×横×高さ÷2　←[1]
底面と上面の2つ分を加味するため底面積を×2 → (縦×横×高さ÷2)×2=底面積 ←[2]

＊側面積＊
側面を展開すると四角形になる ←[3]
四角形の面積の求め方で側面積を出す → 縦×横
立体の高さを“縦”にしたとき、“横”は三角形の三辺の長さの合計になる → 三角形の三辺の長さの合計×立体の高さ=側面積　←[4]

最後に底面積(上面と底面の2つ分)と側面積を足し合わせれば三角柱の表面積が求められます。
角柱のなかでも四角柱は、「直方体」と呼ばれ、より簡単に表面積の計算ができます。すべての辺の長さが等しい(面の大きさと形が同じ)「立方体」はとくに簡単です。公式として覚えてしまっても良いでしょう。

■四角柱(直方体)：(縦×横＋縦×高さ＋横×高さ)×2
直方体は、すべての面が四角形であり向かい合っている面が同じ形・大きさです。同じ大きさの四角形のペア3組を組み合わせてできた立体ともいえます。そのため3つの四角形の面積をもとめてそれを2つずつで足し合わせれば求められるのです。

■立方体：一辺×一辺×6
立方体は、すべての辺の長さが等しい・すべての面の大きさと形が同じ立体でした。そのため一つの面の面積をもとめて立体の面の数である6つ分ほどかければいいのです。
しかも立方体の面は正方形でした。つまり縦も横も同じなので、一辺×一辺で求めた正方形の面積を×6すると求められます。

＊「錐台」に注意＊
底面と上面の形は一緒(相似)であっても、大きさが違い(合同でなく)、太さが一定でない立体を目にする機会もあるでしょう。
下で説明する「錐体」の上側に平行線を入れてスパッと切ったような形で、プリンのような形状といえばイメージがしやすいかもしれません。こういった立体を「錐台(すいだい)」と呼び、柱体と区別されています。仮に底面と上面が相似な四角形で柱の形をしていても、底面と上面の大きさが違って合同でなければ(太さが一定でなければ)柱体ではありません。“四角錐台”と呼ばれる立体です。表面積の求め方も柱体とは異なるため注意しましょう。

「円柱」の表面積

円柱は、底面と上面が合同で太さが一定になっている、底面が円の立体です。「底面積＋側面積＝表面積」の基本形にのっとって、底面と側面の面積を求めて足し合わせましょう。円柱も、底面と同じ面が上下で二つ分ある点に注意してください。こちらもポイントを4つ整理してみました。
[1]底面の形に合わせて計算方法が変わる点
[2]底面と合同な上面もあるため底面積を×2にする点
[3]側面を展開したときには四角形(長方形)になる点
[4]底面の円周の長さと立体の高さを掛け合わせて側面積を求める点

＊底面積＊
底面は円 → 円の面積＝半径×半径×円周率(π：3.14…)　←[1]
底面と上面の2つ分を加味するため底面積を×2 → (半径×半径×円周率)×2=底面積の合計　←[2]

＊側面積＊
側面を展開すると四角形になる ←[3]
四角形の面積の求め方で側面積を出す → 縦×横
立体の高さを“縦”にしたとき、“横”は底面の円周の長さになる → 底面の円周の長さ×立体の高さ → (底辺の直径[半径2つ分]×円周率)×立体の高さ　←[4]

最後に底面積の合計(上面と底面の2つ分)と側面積を足し合わせれば円柱の表面積が求められます。
円の面積を求める「半径×半径×円周率(π：3.14…)」や円周の長さを求める「底辺の直径(半径2つ分)×円周率」が分からないと問題には対応できません。忘れた・覚えていない人は以前の教科書などを使って復習しましょう。また円柱については別記事でも解説をしています。下のリンクから合わせて確認してみてください。

「角錐」の表面積

続いては上にいくにつれて太さが変わって尖った針のような形の立体である「錐体」をチェックしましょう。柱体と同じく、錐体も底面の形に合わせて“◯錐”と呼ぶのでした。最初は底面が多角形である「角錐」について確認しましょう。「底面積＋側面積＝表面積」の基本形にのっとって、底面と側面の面積を求めて足し合わせるのは角柱・円柱とかわりません。
しかし底面から上にいくにつれて太さが変わり最後は点になってしまいます。そのため角柱・円柱のように底面積を二つ分とる必要はありません。さらに上に尖っているため、角錐の場合は側面が三角形になります。ポイントをまとめましたので、ひとつずつチェックしてみてください。
[1]底面の形に合わせて計算方法が変わる点
([2]上面がなく底面だけため、底面積を×2にはせずに一つ分だけで計算する点[柱体のように底面積を二つ分とらない])

[3]側面を展開したときには三角形になる点
[4]側面をつくる三角形すべての面積を足し合わせて側面積を求める点
四角錐の場合をチェックしてみましょう。

＊底面積＊
底面は四角形 → 四角形の面積＝縦×横　←[1]
(上面はなく底面だけため底面積は一つ分だけ ←[2])

＊側面積＊
側面を展開すると三角形になる ←[3]
三角形の面積の求め方で側面積を出す → 縦×横×高さ÷2=底面積
四角錐の場合、側面は4つの三角形
→4つの三角形の面積を足し合わせて側面積を出す
→(縦×横×高さ÷2)＋(縦×横×高さ÷2)＋(縦×横×高さ÷2) +(縦×横×高さ÷2)=側面積の合計 ←[4] ※側面一面ごと(三角形ごと)で縦・横・高さが変わるのに注意

最後に側面積の合計と底面積を足し合わせれば四角錐の表面積が求められます。

三角錐の表面積がテストなどで問われたときは、全ての面が三角形になるので混乱するかもしれません。底面を変えて(立体を回線させて)みて、「底面積＋側面積＝表面積」の基本に当てはめて計算できないかを検討してみましょう。

また三角錐のなかでも底面も側面もすべて正三角形で作られる「正四面体」は、「一辺×一辺×√3」(一辺をaとして、√3 a^2と書く場合もある)で表面積が簡単に求められます。この公式は下の証明から導けるのですが、中学3年生で習う予定の「直角三角形の比」を用いているので1・2年生には難しいかもしれません。分からなければ無理せずに読み飛ばしてください。

正四面体の4つの面は、すべて辺の長さが同じ三角形である。
つまり正三角形の面積を4倍すれば正四面体の面積は求められる。
一辺の長さをaとすると、正三角形の面積は下のとおりである。

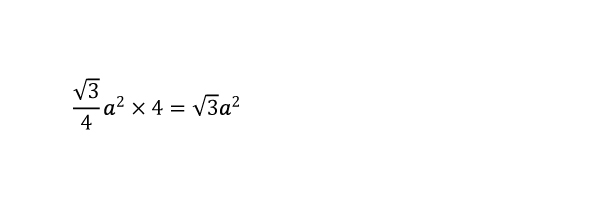
正三角形の面積を4倍すれば正四面体の表面積が求められるので、下のとおり公式が導ける。

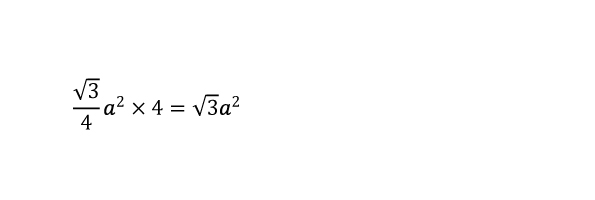
「円錐」の表面積

円錐は、底面が円で、先が尖ったような立体です。「底面積＋側面積＝表面積」の基本形にのっとって、底面と側面の面積を求めて足し合わせて求めてみましょう。円錐は、側面を展開したときに扇形になるのがほかとの違いです。

[1]底面の形に合わせて計算方法が変わる点
([2]上面がなく底面だけため、底面積を×2にはせずに一つ分だけで計算する点[柱体のように底面積を二つ分とらない])
[3]側面を展開したときに扇形になる点
[4]母線(もとの円の半径)と中心角を使って側面積を求める点

＊底面積＊
底面は円 → 円の面積＝半径×半径×円周率(π：3.14…)=底面積　←[1]
(上面はなく底面だけため底面積は一つ分だけ ←[2])

＊側面積＊
側面を展開すると扇形になる ←[3]
扇形の面積の求め方で側面積を出す → 母線(もとの円の半径)×母線×円周率(π：3.14…)×中心角の大きさ÷360=側面積 ←[4]
最後に底面積と側面積を足し合わせれば四角錐の表面積が求められます。

扇形の面積を求めるときに困惑する人が多いかもしれません。まずは扇形の直線で書かれた辺を半径とする円をイメージしてみましょう。下の展開図のようにイメージできたでしょうか。

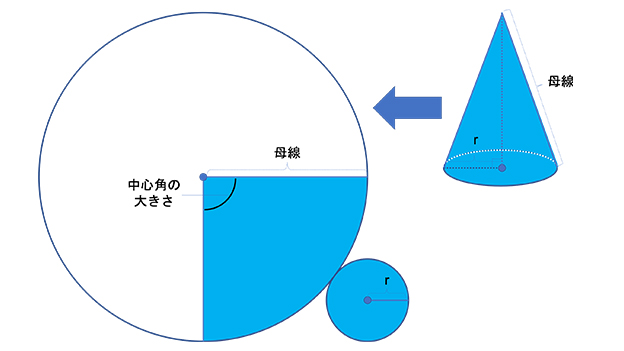
円の面積を求める公式は「半径×半径×円周率」で使い慣れているはずです。求めた円の面積のうち、扇形の部分だけを取り出すと考えてみましょう。求め方は2パターンあります。まずは角度に着目する方法です。角度は合計で360°でした。中心角の大きさと360を比べれば、扇形が円のどれほどかを占めているのかが計算できます。それを示したのが上の[4]で示した式です。

もしくは上の展開図でいうと、大きな円の円周の長さに対する扇形の弧(曲線部分)の長さを計算して活用する方法があります。大きな円と扇形の面積の比を出して、大きな円の面積に掛け合わせれば扇型の面積が求められるのです。大きな円の円周は、母線×2を直径とし、それに円周率をかけて求めます。扇型の弧は、底面の円周と同じで2πrで求められるでしょう。扇型の弧の長さ(底面の円周)÷大きな円の円周で比を求めて、大きな円の面積に掛け合わせれば扇型の面積が計算できます。

「球」の表面積

球は、角や辺のない丸い立体です。どこから見ても同じ形に見えます。球の表面積を求めるときには「半径×半径×円周率×4」(4πr２)の公式を使いますが、これを証明するのは高校生でも難しいです。

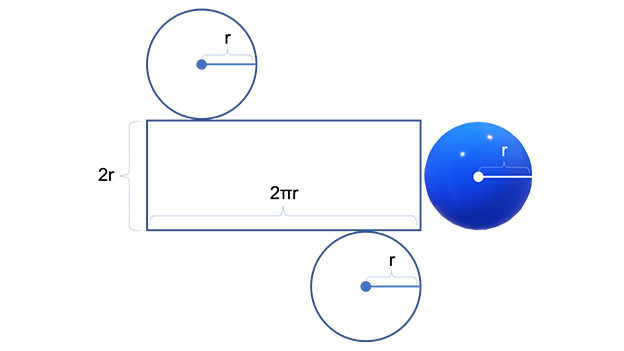
今回は、あくまで公式を覚えるためのイメージを紹介します。半径rの球がぴったり収まる円柱を想像してみましょう。上のイラストのように、テニスボールがケースに収まっているようなイメージです。実は、この円柱の側面積と球の表面積が同じになります。
円柱を展開して考えてみましょう。円柱の側面積は底面の円周×高さで求めるのでした。球の半径rから、底面の円周は2πr・円柱の高さは2rです。よって2πr×2r＝4πr2と球の表面積を求める公式と同じになりました。公式を忘れたときに『そういえば！』と思い出せるきっかけになるかもしれないので、ほかの球でも試して計算してみてください。

立体の表面積を求めてみよう！

基本がおさらいできたら、表面積に関する練習問題に挑戦してみましょう。答えは記事の最後にまとめてあります。
(1)次の展開図からできる立体の名称を答えよ。

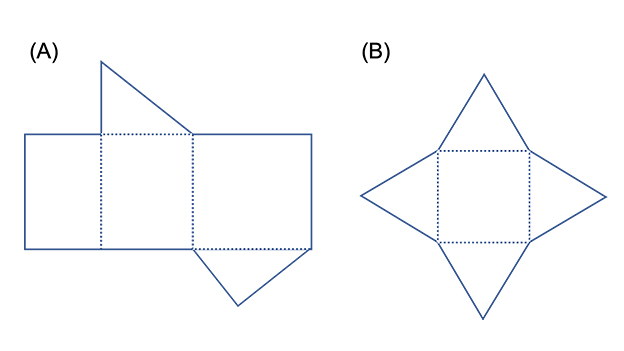
(2)下の図の三角柱の表面積を求めよ。

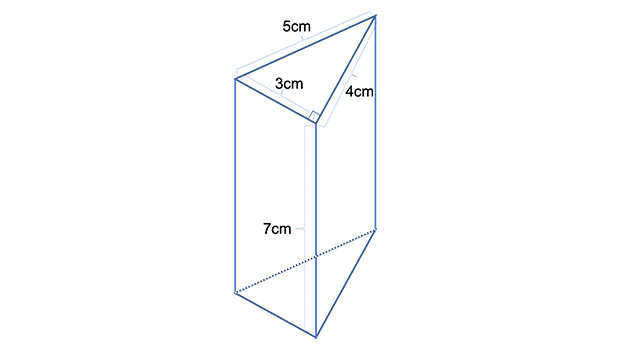
(3)下の図の円柱の表面積を求めよ。

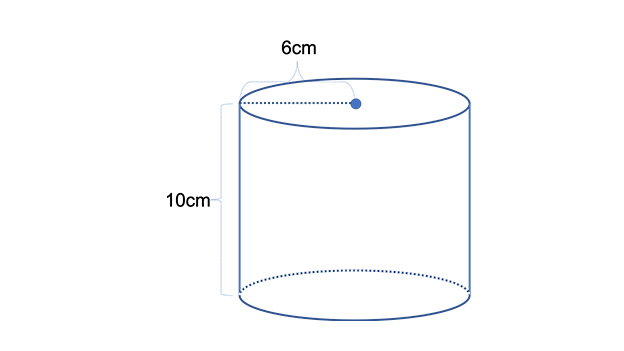
(4)下の図の正四角錐の表面積を求めよ。

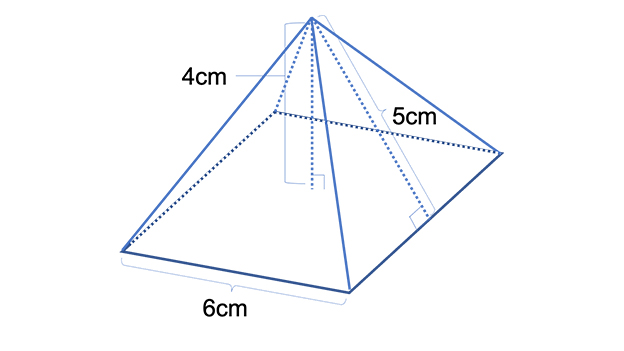
(5)下の図の円錐の表面積を求めよ。

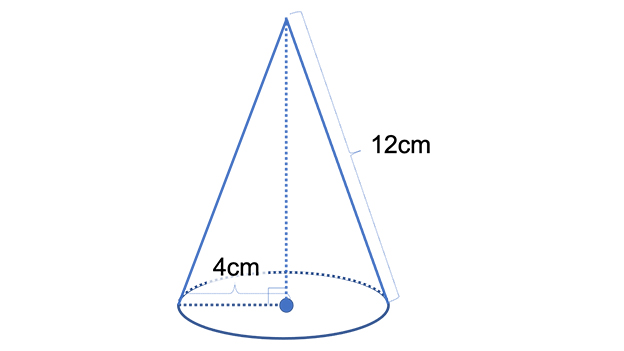
(6)半径が6cmの球について表面積を答えなさい。

表面積とあわせて、体積の問題も数をこなして慣れよう

立体の表面積の求め方や公式をまとめましたが、基本にのっとって丁寧に計算するもよし、公式に当てはめて求めてもよしです。また表面積だけでなく、体積を求める問題とも多く出会うでしょう。問題演習の数をこなして、慣れるのを意識してみてください。

＊練習問題の回答＊
(1)A 三角柱　B四角錐
(2)96㎠
(3)192π㎠
(4)96㎠
(5)64π㎠
(6)144π㎠