【高2数学】ベクトルとは？意味・性質・内積について解説

高校数学を勉強していると「ベクトル」の分野でつまずく人が一定数います。初めて勉強する方にとって、ベクトルの概念はあまりに新しく、慣れるまでに時間がかかるからだと言われています。

しかし、基本的な性質さえ押さえてしまえば、難しい分野ではありません。この記事では、ベクトルの意味・基本的な性質・内積について解説します。

＜この記事で紹介していること＞
・ベクトルの意味
・基本的な性質
・内積の計算方法
・練習問題

ベクトルの意味

「ベクトル」という言葉は、数学の分野だけでなく日常生活やビジネスシーンでも使われます。日常生活やビジネスシーンでは、以下のような使われ方をします。

・「チーム間のベクトルを合わせてこのプロジェクトを乗り切ろう！」
・「目標達成のためには、チーム全員が同じ方向にベクトルを向けなければならない」
・「本をたくさん読むと、ベクトルの異なる発想を得られる」

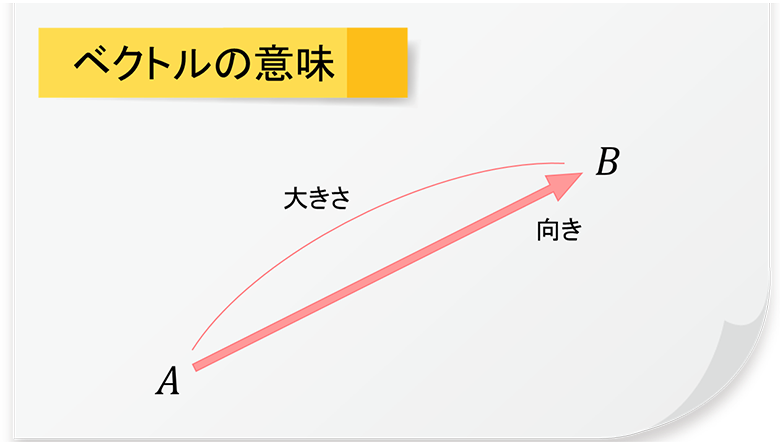
この場合、考え方の傾向・目標達成に向けての姿勢などの意味合いが強いでしょう。一方、数学で使われるベクトルは「向き」と「大きさ」を表します。図にすると以下のように表現できます。

矢印が長いほどベクトルが大きくなるという点を覚えておきましょう。

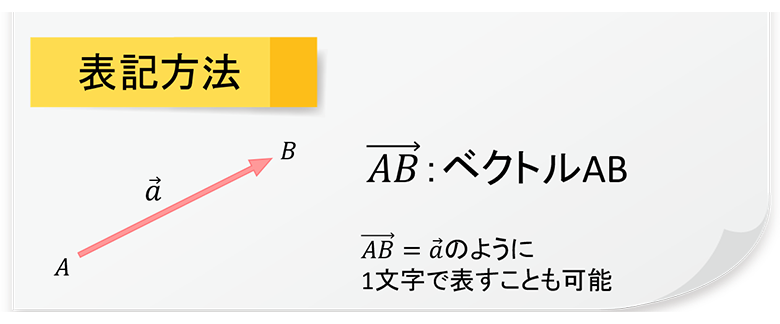
ベクトルの表記方法

ベクトルを数学で扱う以上、数式での表記方法があったほうが便利だと思う方は多いでしょう。始点Aから終点Bに向かうベクトルは以下のように表記されます。

ベクトルの平行移動

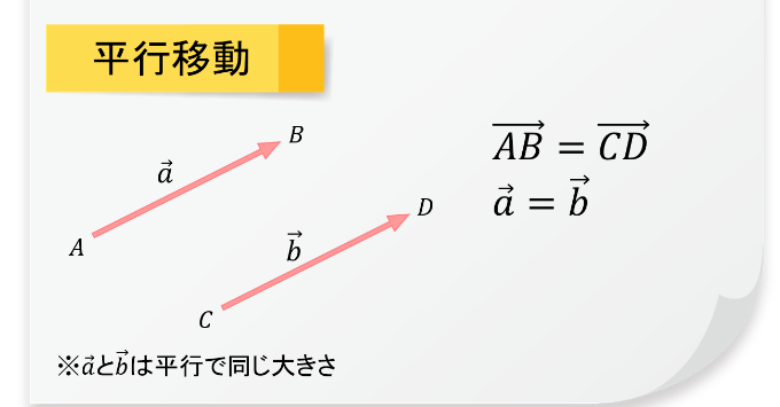
ベクトルの特徴的な性質の1つが「位置に依存しない」という点です。前述したとおり、ベクトルは「向き」と「大きさ」を表します。

つまり、向きと大きささえ一致すれば、別の場所にあっても同じベクトルとして扱われます。そのため、複製したベクトルを平行移動したとしても、数学上では2つのベクトルを同じものとして扱うのです。

ベクトルの成分表示

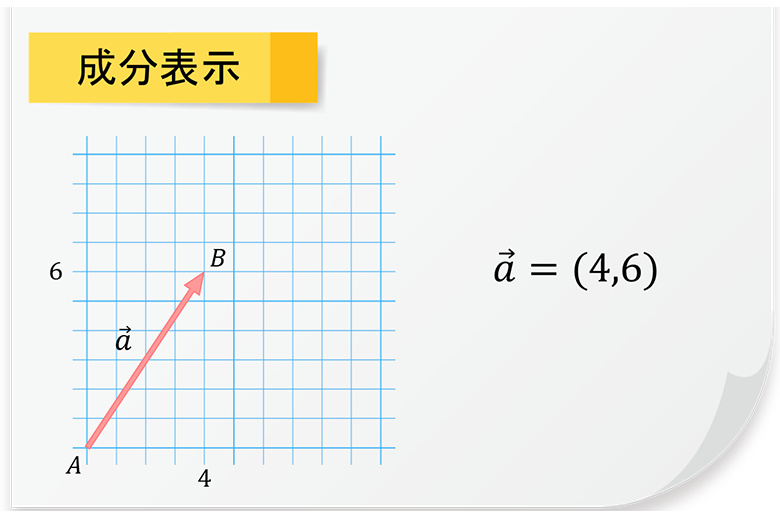
成分表示は、ベクトルの始点を原点に合わせたときに決まる終点の座標です。上図のようなベクトルの場合、x成分が+4、y成分が6で(4,6)と書き表せます。xとyの2成分があれば、どのようなベクトルでも平面上に表せます。

ベクトルの性質

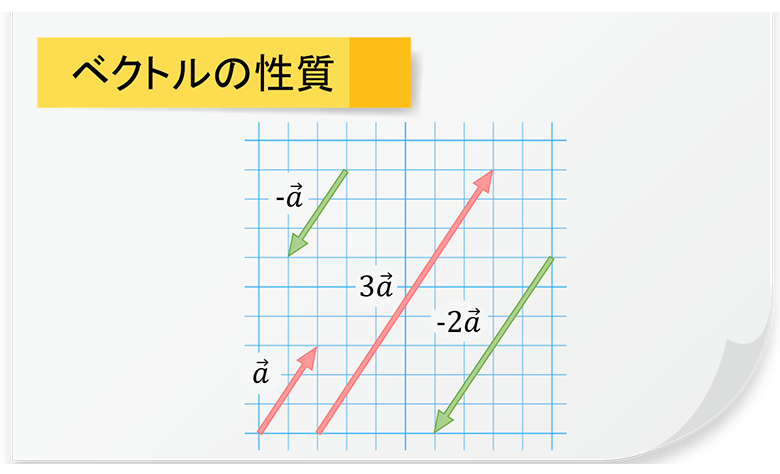
ベクトルには実数をかけることができます。また、ベクトル同士の加減算にも対応しています。実数の「3」をかけたベクトルは元の大きさの3倍です。

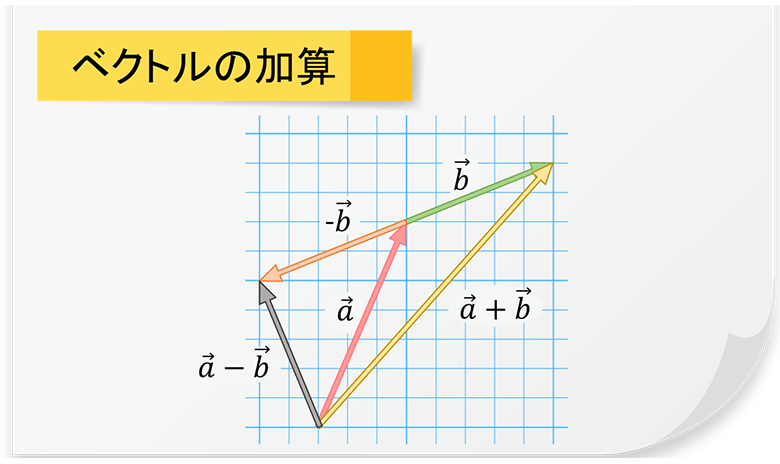
もちろん、マイナスをかけることもできます。マイナスをかけたベクトルは元の逆向きです。ベクトルにベクトルを足すと下図のように、2つのベクトルが連結します。引き算の場合は逆向きのベクトルを足し合わせます。

ベクトルの内積

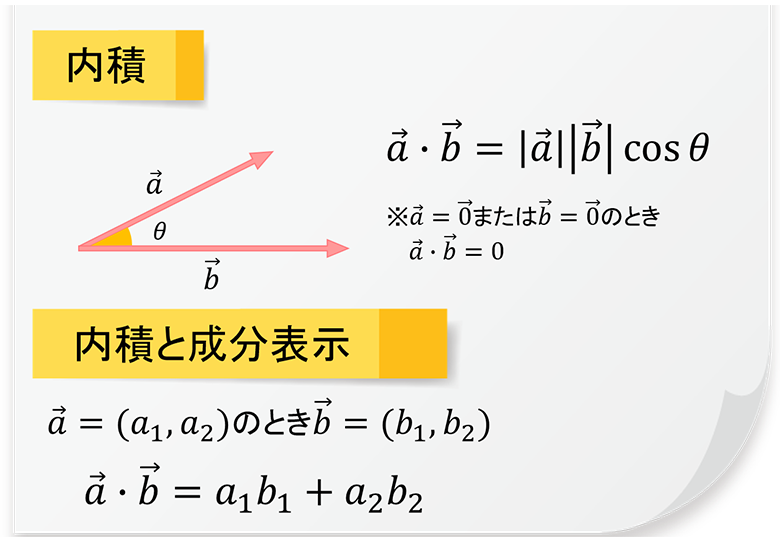
ベクトル同士の加減算は存在しますが、かけ算や割り算はありません。しかし、代わりに「内積」と呼ばれる計算が可能です。内積の定義と成分との関係は上図のとおりです。

定義のとおり、2つのベクトルの内積は、それぞれの大きさとなす角θのcosをすべてかけあわせたものと一致します。通常のかけ算の場合「・」を省略できますが、内積の場合は省略できません。

また、かけ算で度々使われる「×」は、内積では使用できません。ベクトルの内積は、成分表示を使用すると簡単に計算できます。

2つのベクトルのx成分とy成分が分かっている問題であれば、x成分同士の積とy成分同士の積を足し合わせるだけで求められます。

練習問題

実際に手を動かして、ベクトルの問題を解いてみましょう。

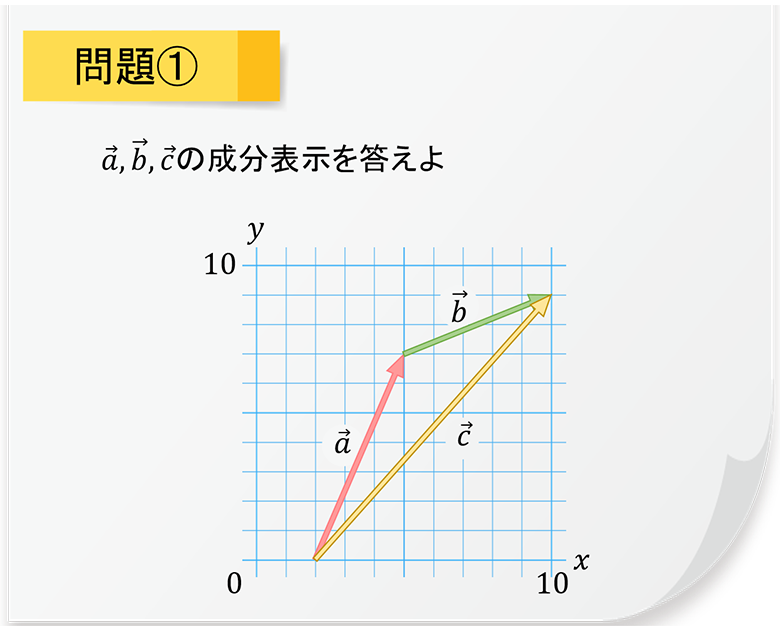
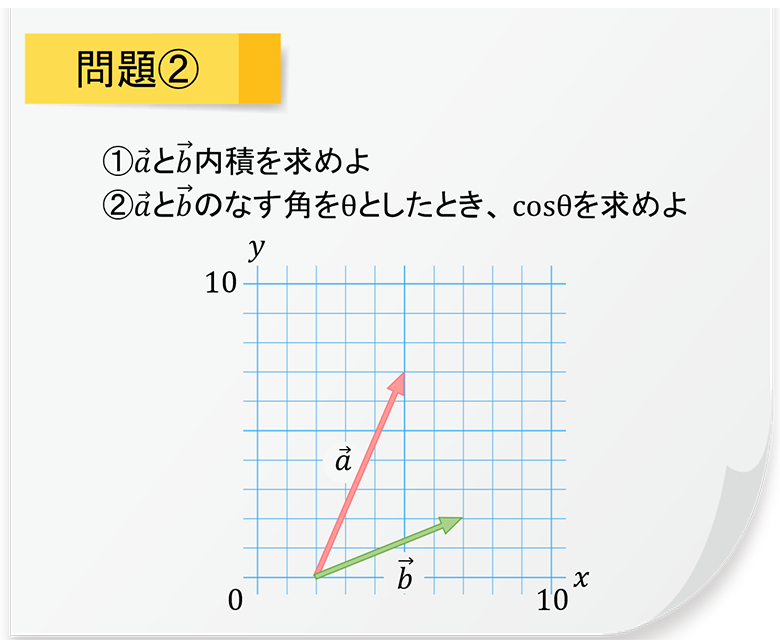
解答は以下のとおりです。

数学が苦手な人は『個別指導塾スタンダード』がおすすめ

ベクトルはcosや絶対値の計算が出てくるため、計算ミスでつまずく学生さんが多くいらっしゃいます。この記事で紹介した内容には公式があまり出てきませんでしたが、学習が進むといくつもの公式を覚えなければなりません。

複雑な問題を解く場合は、図に書き込みながら解き進める必要があるでしょう。ベクトルはただの計算とは違う分野で、慣れるまで時間がかかる方もいるでしょう。

解けない問題を1人で延々と考え続けても勉強は捗りません。勉強の効率を上げるには、わからない部分をそのままにするのではなく、すぐに誰かに教えてもらう必要があります。

高校数学は授業のスピードが速いため、自主学習しないとついていけなくなる場合があります。少しでも数学に苦手意識を感じるのあであれば、塾に通いながらの勉強がおすすめです。

わからないポイントを一つひとつ解決し、応用問題でも解けるようにサポートを受けられます。『個別指導塾スタンダード』では、オーダーメイドのカリキュラムと呼ばれる自由度の高い学習環境を提供しています。

生徒のみなさん一人ひとりに合わせた指導をおこなっているため、自分のペースで学習を進められるでしょう。無料体験授業も実施しているため、ぜひ下のリンクからお近くの教室を確認してみてください。

近くの教室をチェックしてみる

ベクトルは書いて覚えよう

ベクトルは、向きや大きさなどの平面上や空間上の情報を扱った分野です。数式だけでなく図を用いて解く必要があるため、慣れるまでに時間がかかるでしょう。

テストで高得点をとるためには、実際に図や数式を書いて解くようにしましょう。『個別指導塾スタンダード』では無料体験授業を実施しています。

下のリンクから近くの教室をチェックできるため、ぜひ気軽にお試しください。

近くの教室をチェックしてみる