三角形の｢合同条件｣とは!?直角三角形の2つも覚えて証明問題を攻略しよう!!

中学校の数学は暗記で差がつきます。問題にはパターンがあり、新しく出てくる公式や定理などと合わせて覚えてないと解けない(回答するのに時間がかかる)場合が多いです。

とくに照明問題では基本事項の暗記をできているかが出来・不出来に大きく関わります。今回は三角形の合同条件について覚えておきたい要点をまとめました。しっかり頭に入っているか確認してみてください。

三角形の合同とは大きさも形も同じ図形同士の関係性

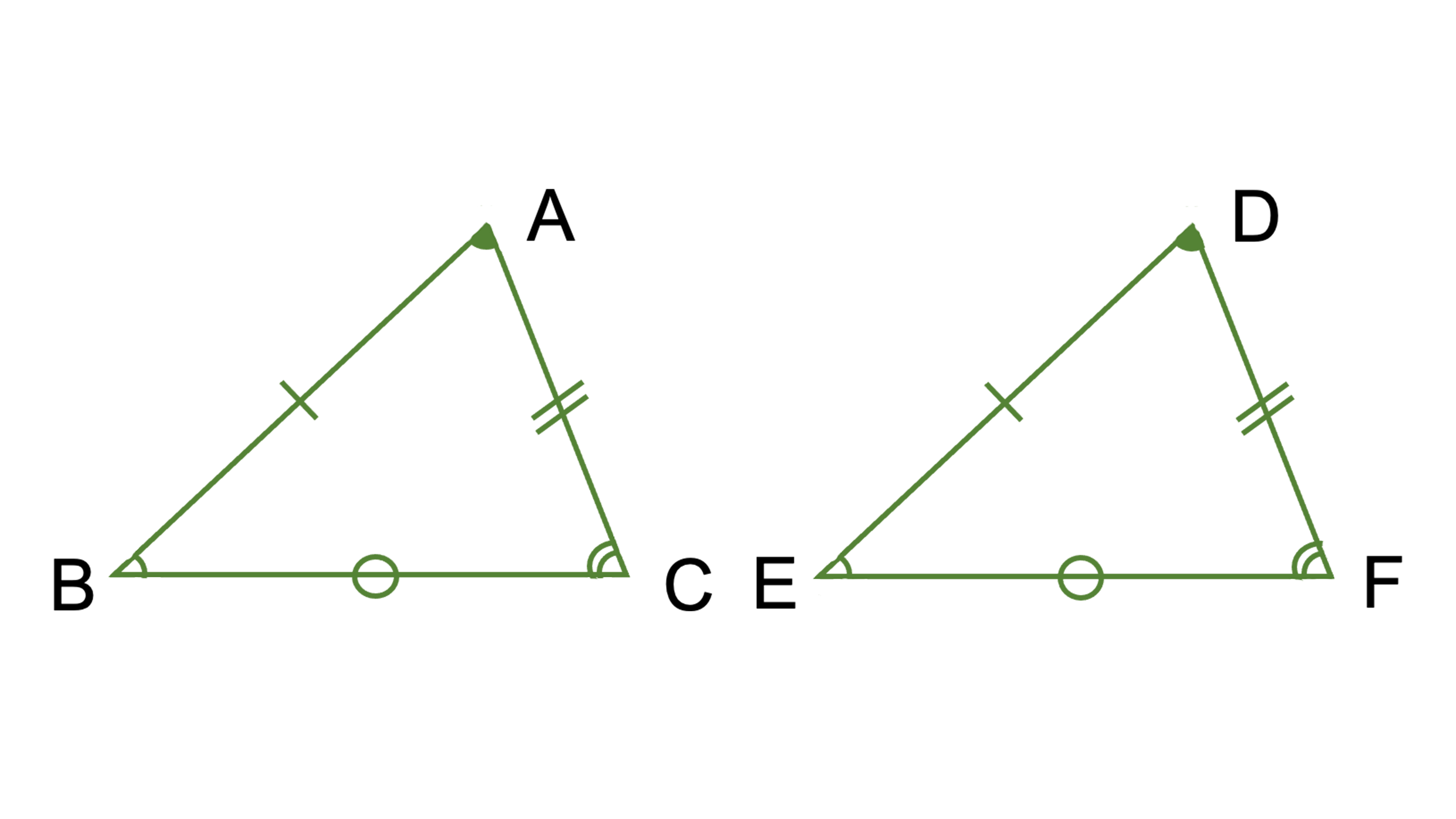
合同とは、形や大きさが全く同じ図形同士の関係性を表す言葉です。向きや位置の関係で違う図形のように見えたとしても、紙で図形2つを切り出してみたら重なり合います。

「≡」の記号を使って合同な三角形同士を示します。上の画像にある2つの三角形であれば「△ABC≡△DEF」と書くと覚えてください。このとき“対応する”頂点の並びと同じ順番で書くのも覚えましょう。上の画像で表せば、△ABC≡△FEDでは対応する点の順番になっていないため間違いで、△ABC≡△DEFと書くのが正解です。

また「対応する」とは、図形で同じ位置にくる点や辺のペアの関係を示す際に使われる表現です。合わせて覚えておきましょう。

3つある三角形の合同条件とは

合同な三角形同士には一定の条件が3つ当てはまります。決まり文句としてそのまま書くようにしてください。

●3組の辺がそれぞれ等しい
※上の三角形ABCと三角形DEFでいえばAB=DE、BC=EF、CA=FD

●2組の辺とその間の角がそれぞれ等しい
※上の三角形ABCと三角形DEFでいえばAB=DE、BC=EF、∠ABC=∠DEF

●1組の辺とその両端の角がそれぞれ等しい
※上の三角形ABCと三角形DEFでいえばAC=DF、∠ACB=∠DFE、∠BAC=∠EDF)

三角形の合同条件で間違いやすいポイント

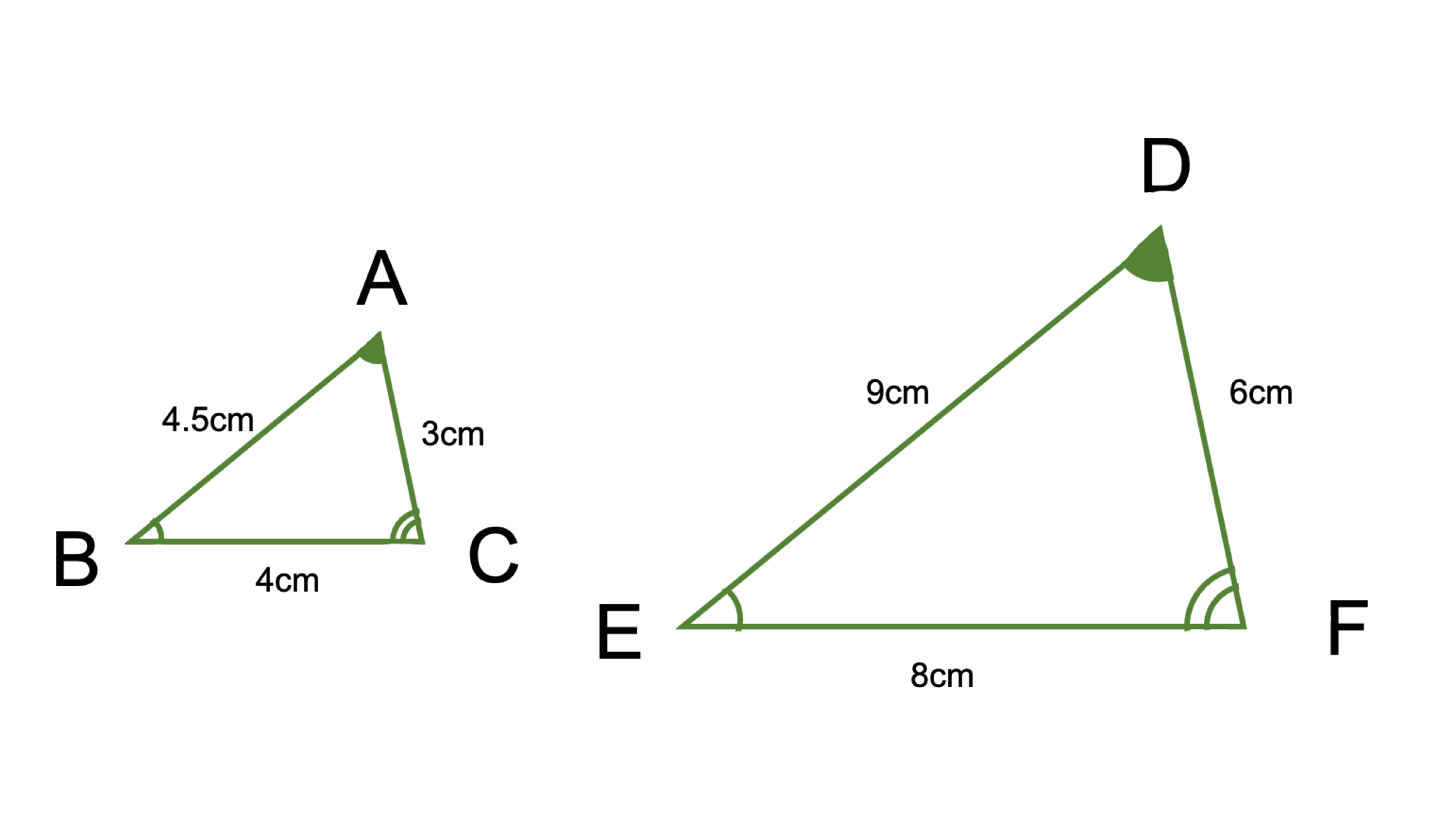
「対応する頂点を同じ順番で書く」と「合同条件は決まり文句としてそのまま書く」を合同条件に関する問題での注意点として紹介しました。加えて、相似と混同する場合があるためしっかり区別しましょう。形も大きさも同じ関係を表す合同に対して、相似とは形は同じだが大きさが違う図形同士の関係を表す言葉です。

-------------------------------
【△ABC∽△DEFになる相似条件】
■３組の辺の比がすべて等しい

※上の三角形ABCと三角形DEFでいえばAC：DF＝CB：FE= BA：ED
■２組の辺の比とその間の角がそれぞれ等しい
※上の三角形ABCと三角形DEFでいえばAB：DE＝BC：EF、∠ABC=∠DEF）
■2つの角が等しい
※上の三角形ABCと三角形DEFでいえば∠ABC=∠DEF、∠ACB=∠DFE)
-------------------------------

相似の条件を3つ上にまとめましたが、合同条件と似ていて混同するかもしれません。「合同＝形・大きさともに同じ」と「相似＝形が同じだが大きさは違う」のそもそもの違いを理解して、合同条件や記号の書き間違いに注意しましょう。

三角形の合同条件を使う問題にチャレンジ！

基本を覚えたら、練習問題に挑戦しましょう。合同条件を一言一句正確に書くのはもちろん、与えられた問題の文章や図形からどの合同条件に導けばいいのかを意識して問題を解いてみてください。

■基礎問題
【1】下の図で、2つの三角形は合同です。このとき次の問いに答えなさい。

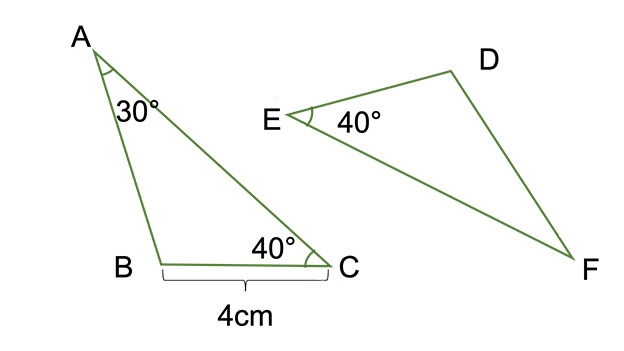
(1)この2つの三角形が合同であることを、記号≡を使って表しなさい。
(2)辺DEの長さを求めなさい。
(3) ∠Dの大きさを求めなさい。

【2】任意の△ABCと△DEFにおいて、次の条件にそれぞれどのような条件を加えると△ABC≡△DEFになりますか。
(1)AB=DE、AC＝DF　→→ ___ または ___
(2)BC=EF、∠C=∠F　→→ ___ または ___

■応用問題
【3】下の図で、線分ABとCDがおたがいの中点Oで交わっています。この図で合同な三角形の組を記号≡を使って表しなさい。またそのとき使った合同条件をいいなさい。

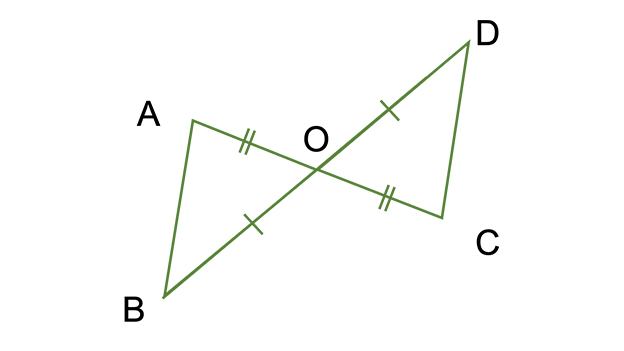
(1)三角形の組
(2)合同条件

【4】次の△ABCと△DEFは、かならず合同であるといえますか。
(1)等しい2辺の長さが8cmになるようにかいた二等辺三角形ABCと二等辺三角形DEF
(2)1辺の長さが10cmになるようにかいた正三角形ABCと正三角形DEF
(3)3つの内角が90°・20°・70°になるようにかいた直角三角形ABCと直角三角形DEF

直角三角形の合同条件は2つ

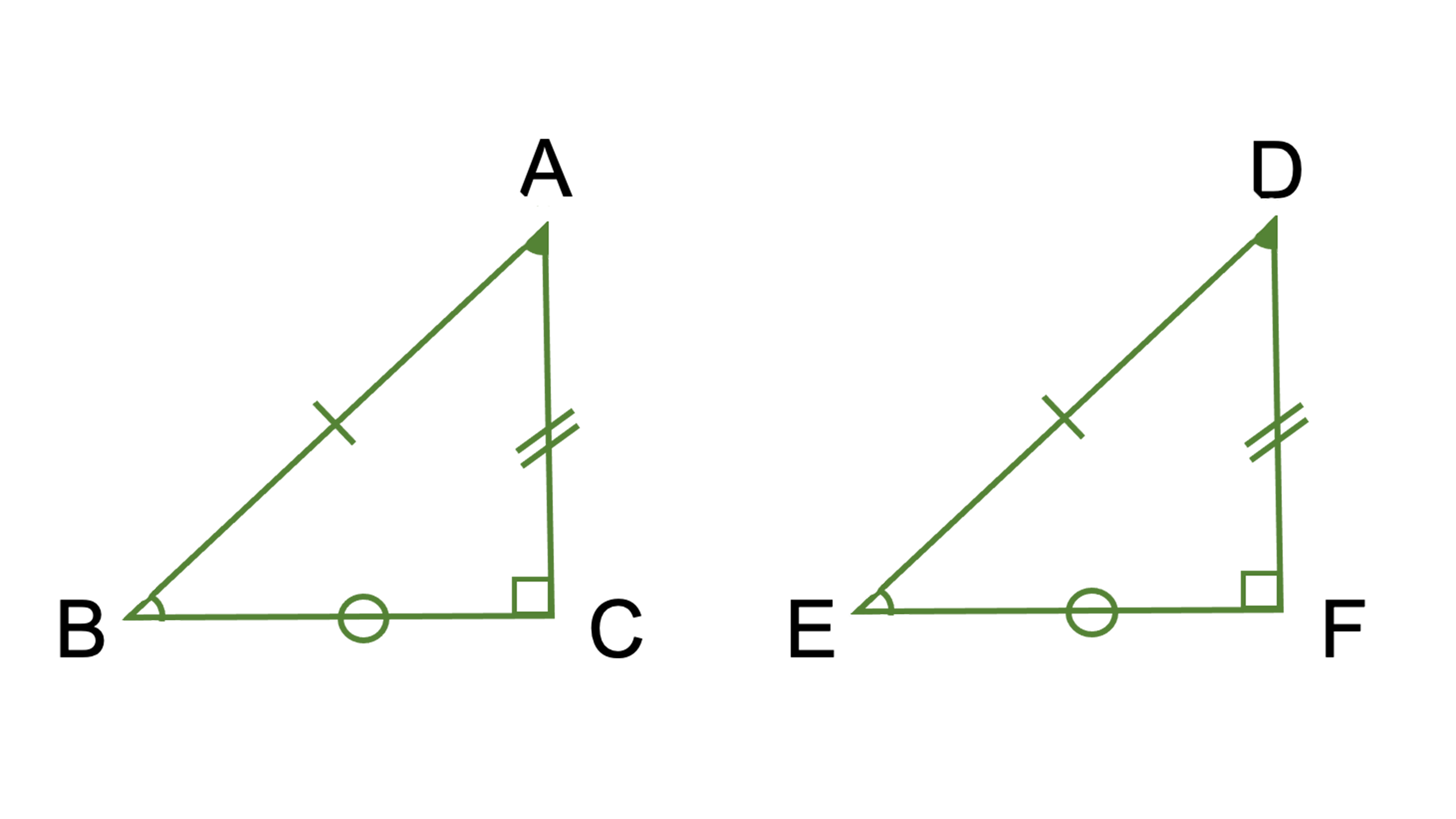
三角形のなかでも直角三角形だけに当てはまる合同条件があります。直角のサインを見つけたら、下の２つの合同条件が使えないか確認するようにしましょう。

●斜辺と1つの鋭角がそれぞれ等しい
※上の三角形ABCと三角形DEFでいえばAB=DE、∠ABC=∠DEF

●斜辺と他の1辺がそれぞれ等しい
※上の三角形ABCと三角形DEFでいえばAB=DE、BC=EF

直角三角形の合同条件を使って問題を解いてみよう

直角三角形の合同条件が出てくる問題にも挑戦しましょう。ほかの三角形の場合と同じく、合同条件の文言は一言一句間違えないように書くのを忘れないように注意してチャレンジしてみてください。

■基礎問題
【5】下の図の2つの直角三角形が合同になることを、次のように証明しました。[ア]〜[ウ]にあてはまるものを答えなさい。

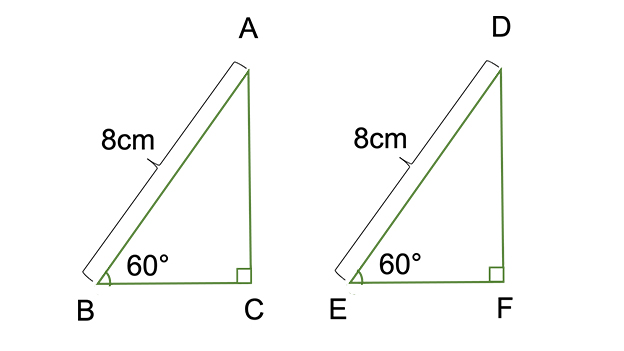
[証明]
△ABCと△DEFで、仮定より、AB＝DE…①　∠B=∠E=60°…②
三角形の3つの内角の和は180°だから、∠A=∠D=180°―(60°＋[ア])＝[イ]…③
①②③から、[ウ]がそれぞれ等しいので、△ABC≡△DEF

【6】AB＝ACの二等辺三角形ABCで、頂点Bから辺ACに垂線をひき、その交点をEとします。このとき、AD=AEになることを証明しなさい。

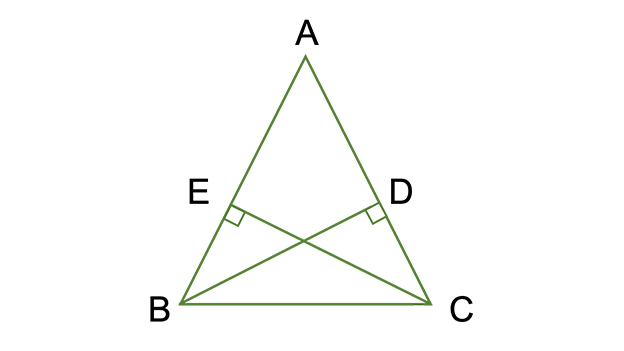
■応用問題
【7】AB＝ACの二等辺三角形ABCで、頂点Bを通り辺ABに垂直な直線と、頂点Cを通り辺ACに垂直な直線との交点をDとし、AとDを結びます。このとき∠ADB＝∠ADCとなることを次のように証明しました。[ア]〜[オ]にあてはまるものを答えなさい。

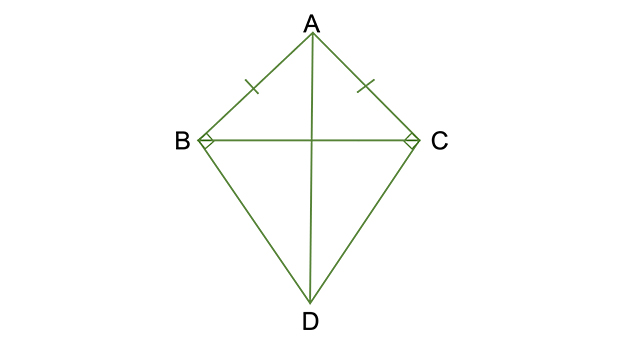
[証明]
△ABDと△[ア]で、仮定よりAB=[イ]…① ∠[ウ]＝∠ACD＝90°…②
ADは共通だからAD＝[エ]…③
①②③から直角三角形の[オ]がそれぞれ等しいので△ABD≡△[ア]
合同な図形では対応する角は等しいので∠ADB＝∠ADC

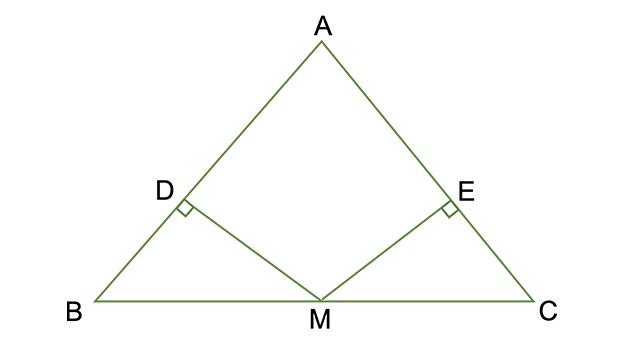
【8】AB=ACの二等辺三角形ABCで、底辺BCの中点Mから辺AB・ACに垂線をひき、その交点をそれぞれD・Eとします。このときMD=MEとなることを証明しなさい。

演習をかさねて合同条件に関する問題のパターンを覚えよう

図形の証明問題に合同条件はよく使われます。問題によって図形はことなりますが、合同条件の文言だけでなく、文章の書き方にも型があって、型にはめていく要素が分かれば機械的な作業で解けます。

要素を見つけられるようになるには多くの問題に挑戦して、問題のパターンを理解しておくのが重要です。ぜひ基本をしっかり押さえながら多くの問題にチャレンジしてみてください。

[練習問題の解答]
▼三角形の合同条件
＊基礎問題＊
【1】(1)△ABC≡△FDE (2)4cm (3)110°
【2】(1)BC=EFまたは ∠A=∠D (2)AC=DFまたは ∠B=∠E (∠A=∠D)
＊応用問題＊
【3】(1)△OAC≡△OBD (2) 2組の辺とその間の角がそれぞれ等しい
【4】(1)いえない (2)いえる　(3)いえない

▼直角三角形の合同条件
＊基礎問題＊
【5】[ア]90° [イ]30° [ウ]1組の辺とその両端の角
【6】△ABDと△ACEで、仮定より、AB=AC…①　∠ADB=∠AEC=90°…②
共通な角だから、∠BAD=∠CAE…③
①②③から、直角三角形の斜辺と1つの鋭角がそれぞれ等しいので、△ABD≡△ACE
合同な図形では、対応する辺は等しいので、AD=AE
＊応用問題＊
【7】[ア]ACD [イ]AC [ウ]ABD [エ]AD [オ]斜辺と他の1辺
【8】△DBMと△ECMで、仮定より、BM=CM…① ∠MDB＝∠MEC=90°…②
二等辺三角形の底辺は等しいので、∠DBM＝∠ECM…③
①②③から直角三角形の斜辺と1つの鋭角がそれぞれ等しいので、△DBM≡△ECM
合同な図形では対応する辺は等しいので、MD=ME